Two rods, one made of copper and the other steel of the same length and cross sectional area are joined together. (The thermal conductivity of copper is 385J.s−1.m−1.K−1 and steel is 50J.s−1.m−1.K−1.) If the copper end is held at 100∘C and the steel end is held at 0∘C, what is the junction temperature (assuming no other heat losses) ?
0.12
0.5
0.73
0.88
The correct Answer is:D
To find the junction temperature of the two rods made of copper and steel, we can use the concept of thermal conductivity and heat flow. Here’s a step-by-step solution:
Step 1: Understand the Setup
We have two rods:
- Rod 1 (Copper): Thermal conductivity K1=385J.s−1m−1K−1
- Rod 2 (Steel): Thermal conductivity K2=50J.s−1m−1K−1
Both rods have the same length L and cross-sectional area A. The copper end is maintained at 100∘C and the steel end at 0∘C.
Step 2: Set Up the Heat Current Equation
The heat current Q flowing through both rods must be equal since they are in steady state (no heat loss). We can express the heat current through each rod as:
Q=(T1−Tj)R1=(Tj−T2)R2
Where:
- T1=100∘C (temperature at the copper end)
- T2=0∘C (temperature at the steel end)
- Tj = junction temperature
- R1 and R2 are the thermal resistances of copper and steel respectively.
Step 3: Calculate the Thermal Resistance
The thermal resistance R for each rod can be calculated using the formula:
R=LK⋅A
Thus, we have:
- For copper: R1=LK1⋅A
- For steel: R2=LK2⋅A
Step 4: Express the Heat Current
Substituting the resistances into the heat current equations, we get:
(100−Tj)LK1⋅A=(Tj−0)LK2⋅A
Step 5: Simplify the Equation
Since L and A are common in both terms, they can be canceled out:
(100−Tj)⋅K1L=Tj⋅K2L
This simplifies to:
(100−Tj)⋅K1=Tj⋅K2
Step 6: Rearrange the Equation
Rearranging gives us:
100K1=Tj(K1+K2)
Step 7: Solve for Tj
Now, we can solve for Tj:
Tj=100K1K1+K2
Step 8: Substitute the Values
Substituting the values of K1 and K2:
Tj=100⋅385385+50=38500435
Step 9: Calculate the Junction Temperature
Now, calculating the value:
Tj=38500435≈88.51∘C
Conclusion
Thus, the junction temperature Tj is approximately 88.51∘C.
We have two rods:
- Rod 1 (Copper): Thermal conductivity K1=385J.s−1m−1K−1
- Rod 2 (Steel): Thermal conductivity K2=50J.s−1m−1K−1
The heat current Q flowing through both rods must be equal since they are in steady state (no heat loss). We can express the heat current through each rod as:
- T1=100∘C (temperature at the copper end)
- T2=0∘C (temperature at the steel end)
- Tj = junction temperature
- R1 and R2 are the thermal resistances of copper and steel respectively.
The thermal resistance R for each rod can be calculated using the formula:
- For copper: R1=LK1⋅A
- For steel: R2=LK2⋅A
Substituting the resistances into the heat current equations, we get:
Since L and A are common in both terms, they can be canceled out:
Rearranging gives us:
Now, we can solve for Tj:
Substituting the values of K1 and K2:
Now, calculating the value:
Thus, the junction temperature Tj is approximately 88.51∘C.
Topper's Solved these Questions
Similar Questions
Calculate the thermal resistance of an aluminium rod of length 20cm and area of cross-section 4cm2. The thermal conductivity of aluminium is 210Js−1m−1K−1.
View SolutionThree rods each of same length and cross - section are joined in series. The thermal conductivity of the materials are K, 2K and 3K respectively. If one end is kept at 200∘C and the other at 100∘C. What would be the temperature of the junctions in the steady state? Assume that no heat is lost due to radiation from the sides of the rods.
View Solution
Knowledge Check
Two rods of copper and brass having the same length and cross - section are joined end to end. The free end of the copper is at 0∘C and of brass is at 80∘C in steady-state. If thermal conductivity of copper is 4 times of that of brass find the temp. at junction of two rods
A80∘CB64∘CC20∘CD16∘CTwo wires, out of copper and the other of steel, are of same length and cross section. They are welded together to from a long wire. On suspending a weight at its one end, increment in length is found to be 3 cms. If Young's modulus of steel is double that of copper the increment in steel wire will be
A1 cmB2 cmC1.5 cmD2.5 cmTwo rods of same length and cross section are joined along the length. Thermal conductivities of first and second rod are K1 and K2. The temperature of the free ends of the first and seconds rods are maintained at θ1 and θ2 respectively. The temperature of the common junction is
Aθ1+θ22BK2K2K1+K2(θ1+θ2)CK1θ1+K2θ2K1+K2DK2θ1+K1θ2K1+K2
Heat is flowing through a rod of length 25.0cm having cross-sectional area 8.80cm2. The coefficient of thermal conductivity for the material of the rod is K=9.2×10−2kcals−1m−1.∘C−1. The Temperatures of the ends of the rod are 125∘C and 0∘C in the steady state. Calculate (i) temeprature gradient in the rod (ii) temperature of a point at a distance of 10.0cm from the hot end and (iii) rate of flow of heat.
View SolutionA rod of length1m having cross sections area 0.75m^(2), conducts heat at 6000J/sec.Then the temperature difference across the rod isK=200Wm^(-1)k^(-1)
View SolutionFigure shows a copper rod joined to a steel rod. The rods have equal length and and the equal cross sectional area. The free end of the copper rod is kept at 0∘C and that of the steel rod is kept at 100∘C . Find the temperature at the junction of the rods. conductivity of copper =390WM−1^(@)C^(-1)andtˆofsteel=46Wm^(-1)(∘)C−1 .

View Solution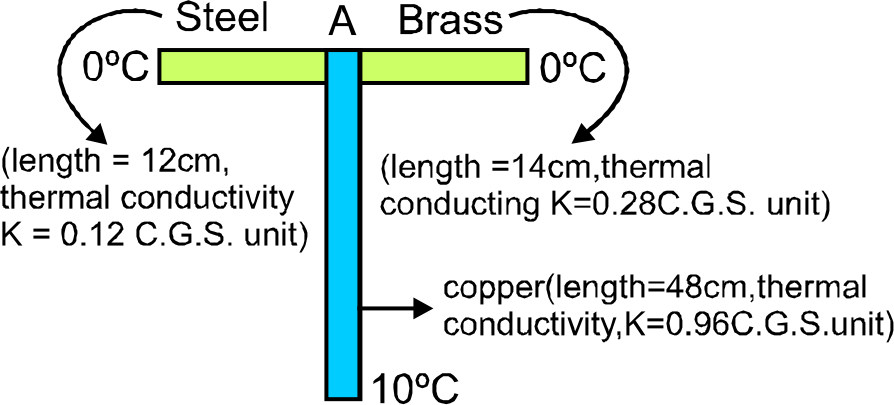
Three rods of copper, brass and steel are joined together to form T shape as shown in figure. The cross sectional area of each rod is 4cm2 the end of copper rod is maintained at 10∘C and the ends of brass and steel rods at 0∘C assume there is no loss of heat to surrounding. What is temperature of junction point A in .∘C
View SolutionTwo bars of same length and same cross-sectional area but of different thermal conductivites K1 and K2 are joined end to end as shown in the figure. One end of the compound bar it is at temperature T1 and the opposite end at temperature T2 (whereT1>T2). The temperature of the junction is

View Solution