We have a thin spherical of radius R. Half of the sphere carrying surface change density σ1 and rest half carrying σ2. Magnitude of force of electromagnetic interaction between hemispherical parts carrying surface charge density σ1 and rest of the hemispherical portion is f0=α×104 Newton. Here α is an integer. Value of α will be.
Given σ1√ε0×102cm/m2,σ2=4σ1,R=√3πm
3
4
5
6
The correct Answer is:D
f=πR22ε0σ1σ2
=π3π12ε04ε0×104=6×104N
Similar Questions
A uniformly charged thin spherical shell of radius R carries uniform surface charge density of sigma per unit area.It is made of two hemispherical shells hold together by pressing them with force F.F is equal to qquad F + + +(1)/(+)+
View SolutionA hemispherical bowl of radius R carries a uniform surface charge density of σ. Find potential at a point P located just outside the rim of the bowl (see figure). Also calculate the potential at a point A located at a distance R/2 from the centre on the equatorial plane.
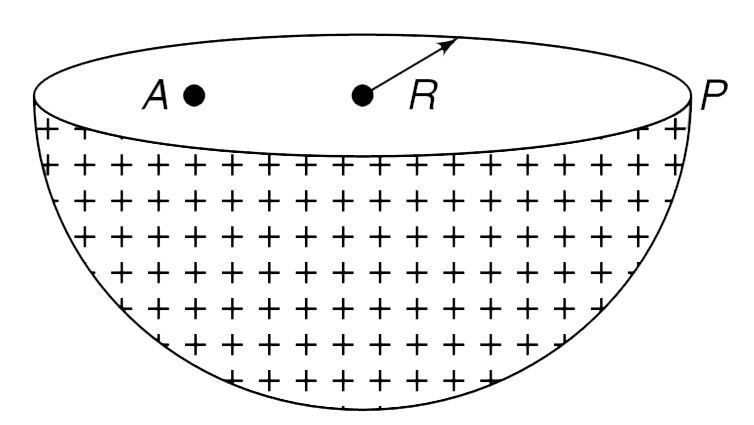
View Solution
Knowledge Check
Two parallel plane sheet 1 and 2 carry uniform charge densities σ1 and σ2 as shown in fig.electric field in the region marked II is (σ1>σ2)
 A−(σ1+σ2)2ε0B−(σ1σ2)2ε0C(σ1+σ2)2ε0D(σ1−σ2)2ε0
A−(σ1+σ2)2ε0B−(σ1σ2)2ε0C(σ1+σ2)2ε0D(σ1−σ2)2ε0Two parallel large thin metal sheets have equal surface charge densities (σ=26.4×10−12C/m2) of opposite signs. The electric field between these sheets is :
A1.5N/CB1.5 xx 10^(-10) N//CC3N/CD3 xx 10^(-10) N//CTwo parallel large thin metal sheets have equal surface charge densities (σ=26.4×10−12C/m2) of opposite signs. The electric field between these sheets is :
A1.5N/CB1.5 xx 10^(-10) N//CC3N/CD3 xx 10^(-10) N//C
64 globules of mercury each of radius. r and carrying q coalesce to form a big globule.Find the ratio between surface charge density of the big globule σ1 and surface charge density of the small globule σ2. σ1σ2 ?
View Solution64 globules of mercury each of radius. r and carrying q coalesce to form a big globule.Find the ratio between surface charge density of the big globule σ1 and surface charge density of the small globule σ2. σ1σ2 ?
View SolutionTwo charged spherical conductors of radius R1 and R2 are connected by a wire. Then the ratio of surface charge densities of the spheres σ1σ2 is
View SolutionA thin spherical shell of radius R is cut into two equal halves and then each of its halves is charged to the same uniform surface charge density σ. If F is the force exerted on each half to keep them at equilibrium, then F is proportional to
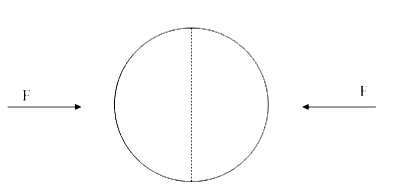
View SolutionTwo parallel large thin metal sheets have equal surface charge densities (σ=26.4×10−12C/m2) of opposite signs. The electric field between these sheets is
View Solution