Two parallel large thin metal sheets have equal surface charge densities (σ=26.4×10−12C/m2) of opposite signs. The electric field between these sheets is
3N/C
1.5×10−10N/C
1.5N/C
3×10−10N/C
The correct Answer is:A
To find the electric field between two parallel large thin metal sheets with equal surface charge densities of opposite signs, we can follow these steps:
1. Identify the Surface Charge Densities:
Let the surface charge density on the positively charged plate be σ=26.4×10−12C/m2 and on the negatively charged plate be −σ=−26.4×10−12C/m2.
2. Understand the Electric Field Due to a Single Plate:
The electric field E due to a single infinite plane sheet of charge with surface charge density σ is given by the formula:
E=σ2ϵ0
where ϵ0 is the permittivity of free space, approximately 8.85×10−12C2/N m2.
3. Calculate the Electric Field from Each Plate:
- For the positively charged plate:
E1=σ2ϵ0
- For the negatively charged plate:
E2=−σ2ϵ0
However, since the electric field direction due to the negative plate is opposite to that of the positive plate, we will consider the magnitudes when calculating the total electric field between the plates.
4. Determine the Total Electric Field Between the Plates:
The total electric field E between the plates is the sum of the electric fields due to both plates:
E=E1+|E2|=σ2ϵ0+σ2ϵ0=σϵ0
5. Substitute the Values:
Now we can substitute the values of σ and ϵ0:
E=26.4×10−128.85×10−12N/C
6. Calculate the Result:
Performing the calculation:
E≈26.48.85×100N/C≈2.98N/C
Final Answer:
The electric field between the two parallel sheets is approximately 2.98N/C.
---
Let the surface charge density on the positively charged plate be σ=26.4×10−12C/m2 and on the negatively charged plate be −σ=−26.4×10−12C/m2.
The electric field E due to a single infinite plane sheet of charge with surface charge density σ is given by the formula:
E=σ2ϵ0
where ϵ0 is the permittivity of free space, approximately 8.85×10−12C2/N m2.
- For the positively charged plate:
E1=σ2ϵ0
- For the negatively charged plate:
E2=−σ2ϵ0
However, since the electric field direction due to the negative plate is opposite to that of the positive plate, we will consider the magnitudes when calculating the total electric field between the plates.
The total electric field E between the plates is the sum of the electric fields due to both plates:
E=E1+|E2|=σ2ϵ0+σ2ϵ0=σϵ0
Now we can substitute the values of σ and ϵ0:
E=26.4×10−128.85×10−12N/C
Performing the calculation:
E≈26.48.85×100N/C≈2.98N/C
The electric field between the two parallel sheets is approximately 2.98N/C.
Topper's Solved these Questions
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Assertion Reason
8 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Section D - Chapter End Test
29 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - AIPMTNEET Questions
38 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Section D - Chapter End Test
29 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
Two parallel large thin metal sheets have equal surface densities 26×10−12C/m2 of opposite signs. The electric field between these sheets is -
View SolutionTwo large thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and magnitude 27×10−22Cm−2. The electric field →E in region II in between the plates is
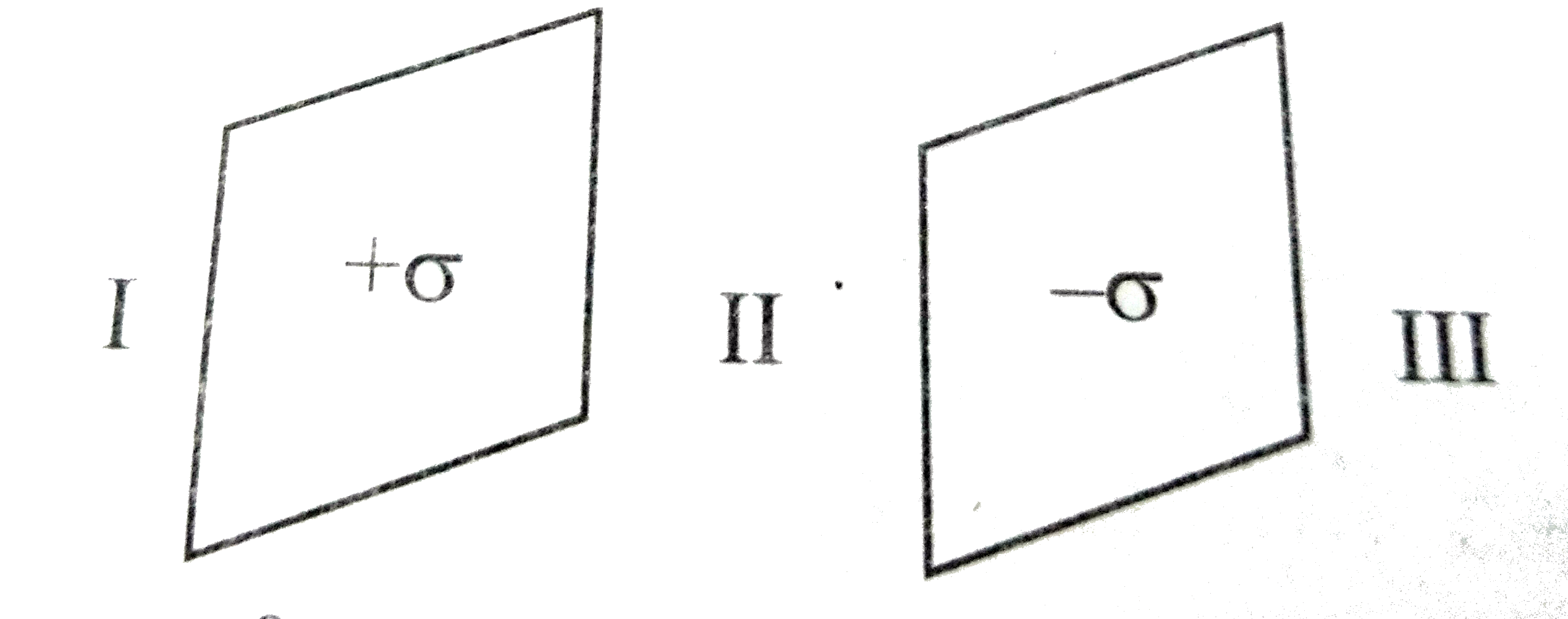
View Solution
Knowledge Check
Two parallel large thin metal sheets have equal surface densities 26.4×10−12C/m2 of opposite signs. The electric field between these sheets is:
A1.5N/CB1.5×10−16N/CC3×10−10N/CD3N/CTwo large, thin plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and of magnitude 16×10−22Cm−2. The electric field between the plates is
A1.8×10−10NC−1B1.9×10−10NC−1C1.6×10−10NC−1D1.5×10−10NC−1Two infinitely long parallel sheets having surface charge densities +σand−σ respectively are separated by a small distance. The electric field in the region between the plates is
A0Bσ2∈0Cσ∈0D2σ∈0
Two large parallel plane sheets have uniform charge densities + σand−σ. Determine the electric field (i) between the sheets, and (ii) outside the sheets.
View SolutionAn infinite thin plane sheet of charge density 7.08×10−11(C/m2) is held in air. Find the electric field at a point very close to the sheet.
View SolutionAn infinite thin plane sheet of charge density 7.08×10−11(C/m2) is held in air. Find the electric field at a point very close to the sheet.
View SolutionTwo infinite sheets of charge carry equal and opposite uniform charge densities ±σ.The electric field in the free space between the two sheets is
View SolutionTwo infinite sheets of charge carry equal and opposite uniform charge densities ±σ.The electric field in the free space between the two sheets is
View Solution
