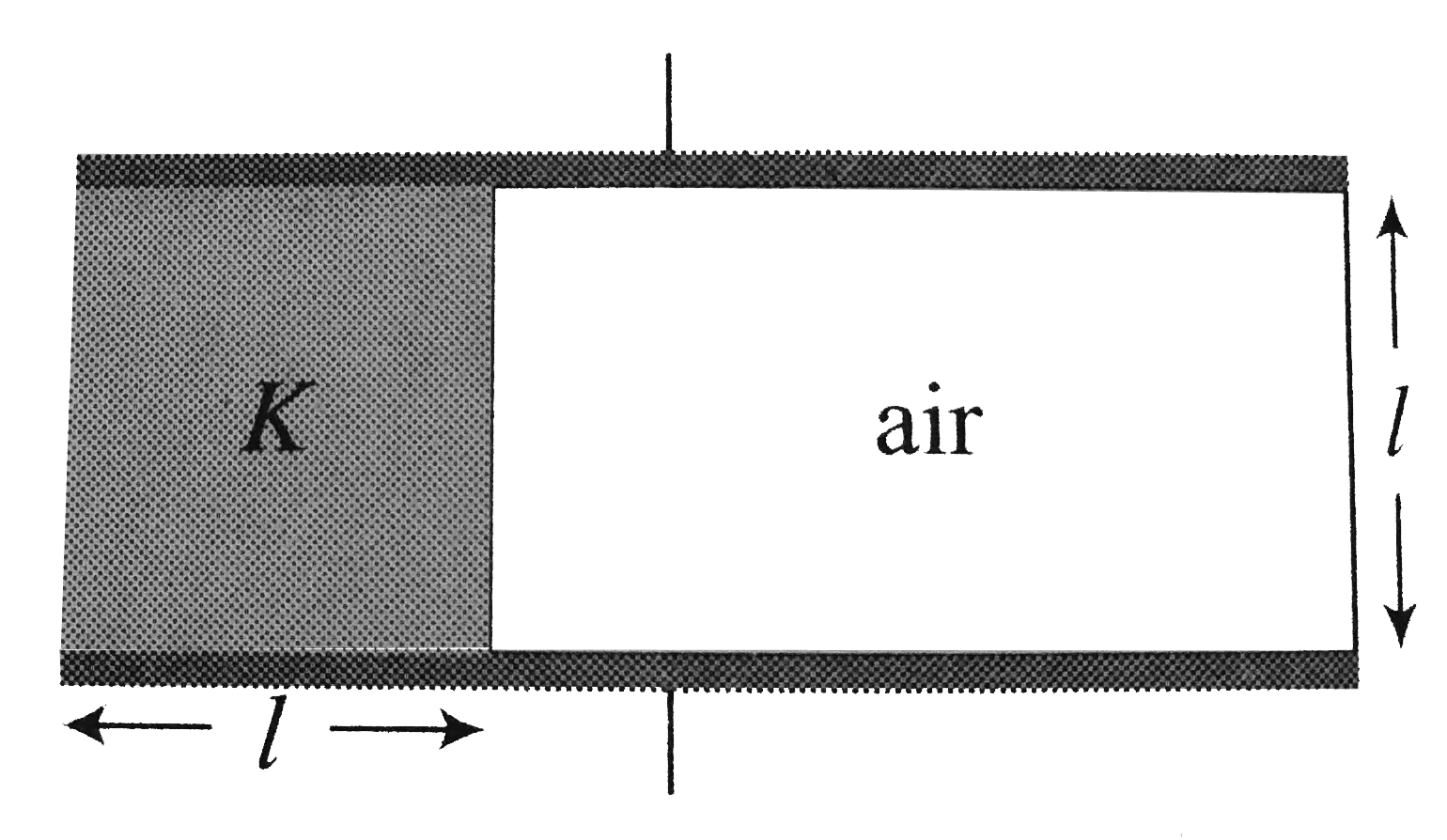
parallel plate capacitor has capacitance C when no dielectric between thw plates. Now a slab of dielectric constant K, having same thickness as the separation between the plates is introduced so as to fill one-fourth of the capacitor as shown in the figure. the new capacitance will be
(K+1)C4
(K+2)C4
(K+3)C4
KC4
The correct Answer is:C
We can observe that system is equivalent to two capacitors C1 and C2 in parallel.

Capacitance of original capacitor without dipole.
C1=ε0d(3A4)=3ε0A4d
With medium, C2=ε0Kd(A4)=ε0AK4d
C'=C1+C2
Or C'=3ε0A4d+ε0AK4d=ε0Ad[34+K4]
Or C'=C4(K+3) [∵C=Aε0d]
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Assertion Reason8videos
ELECTRIC POTENTIAL & CAPACITANCE
- BOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Section D - Chapter End Test29videos
ELECTRIC POTENTIAL & CAPACITANCE
- BOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - AIPMTNEET Questions38videos
ELECTRIC POTENTIAL & CAPACITANCE
- BOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Section D - Chapter End Test29videos
ELECTRIC CHARGE, FIELD & FLUX
- BOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D - Chapter End Test30videos
ELECTROMAGNETIC INDUCTION
Similar Questions
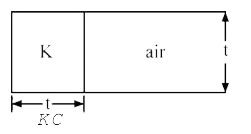
A parallel plate capacitor with air as the dielectric has capacitance C. A slab of dielectric constant K and having the same thickness as the separation between plates is introduced so as to fill one-fourth of the capacitor as shown in the figure. The new capacitance will be :
 View Solution
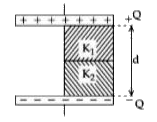
View SolutionTwo dielectric slabs of dielectric constants K1andK2 are filled in between the two plates, each of area A, of the parallel plate capacitor as shown in the figure. Find the net capacitance of the capacitor.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
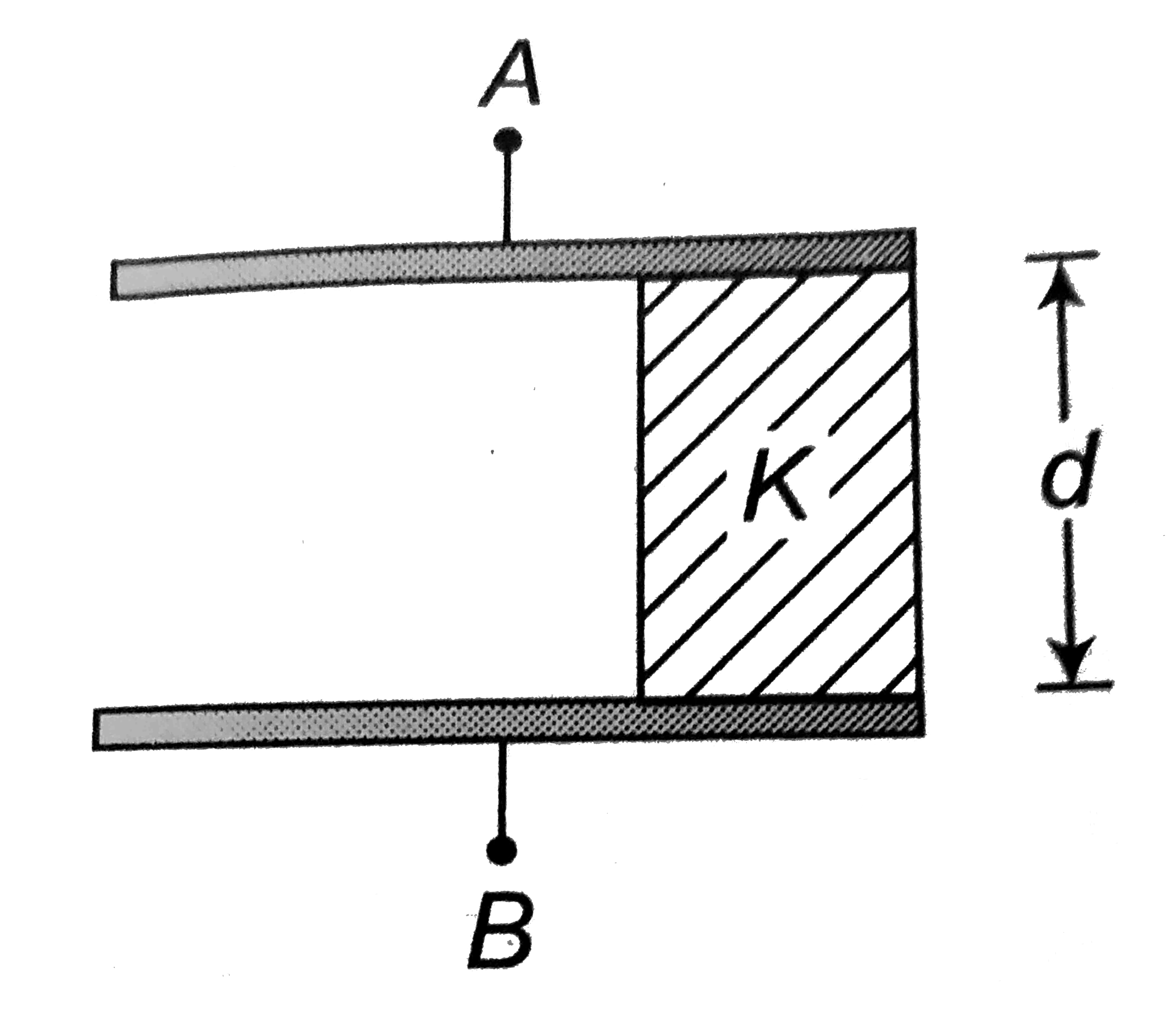
A parallel plate capacitor with vacuum between its plates has capacitance C. A slabe of dielectric constant K and having the same thickness as the separation between the plates is introduced so as to fill 1/3rd of the capacitor as shown in the figure. the new capacitance will be
 A(K+2)c4B(K+2)c3C(K+3)c4D(K+3)c3
A(K+2)c4B(K+2)c3C(K+3)c4D(K+3)c3 - Question 2 - Select One
A parallel -plate air capacitor has capacity C. A dielectric slab of dielectric constant K, whose thickness is half of the air gap between the plates, is now inserted between the plates. The capacity of the capacitor will now be
AKC/2B2KC/(K+1)C2KC/(K−1)DC(K+1)/(K−1) - Question 3 - Select One
A parallel plate air capacitor has capacitance C. Half of space between the plates is filled with dielectric of dielectric constant K as shown in figure . The new capacitance is C . Then
 AC=C[KK+1]BC'=C[2KK+1]CC'=2CK+1DC'=C[1+K2]
AC=C[KK+1]BC'=C[2KK+1]CC'=2CK+1DC'=C[1+K2]
A parallel-plate capacitor with plate area A has separation d between the plates. Two dielectric slabs of dielectric constant K1 and K2 of same area A/2 and thickness d/2 are inserted in the space between the plates. The capacitance of the capacitor will be given by :
 View Solution
View SolutionA parallel plate air capacitor has a capacitance C. When it is half filled with a dielectric of dielectric constant 5, the percentage increase in the capacitance will be
View SolutionA parallel plate capacitor is filled with dielectrics. What is capacitance?
 View Solution
View SolutionA parallel plate air capacitor has a capacitance C. When it is half filled with a dielectric of dielectric constant 5, then the percentage increase in the capacitance will be
 View Solution
View SolutionA parallel plate capacitor with oil as a dielectric between the plates has a capacitance C. if the oil, with dielectric constannt (K=3), is removed, then the capacitance of the capacitor will be
View Solution

