is a variable point on the ellipse whose foci are and . The maximum area (in of the is
The correct Answer is:B
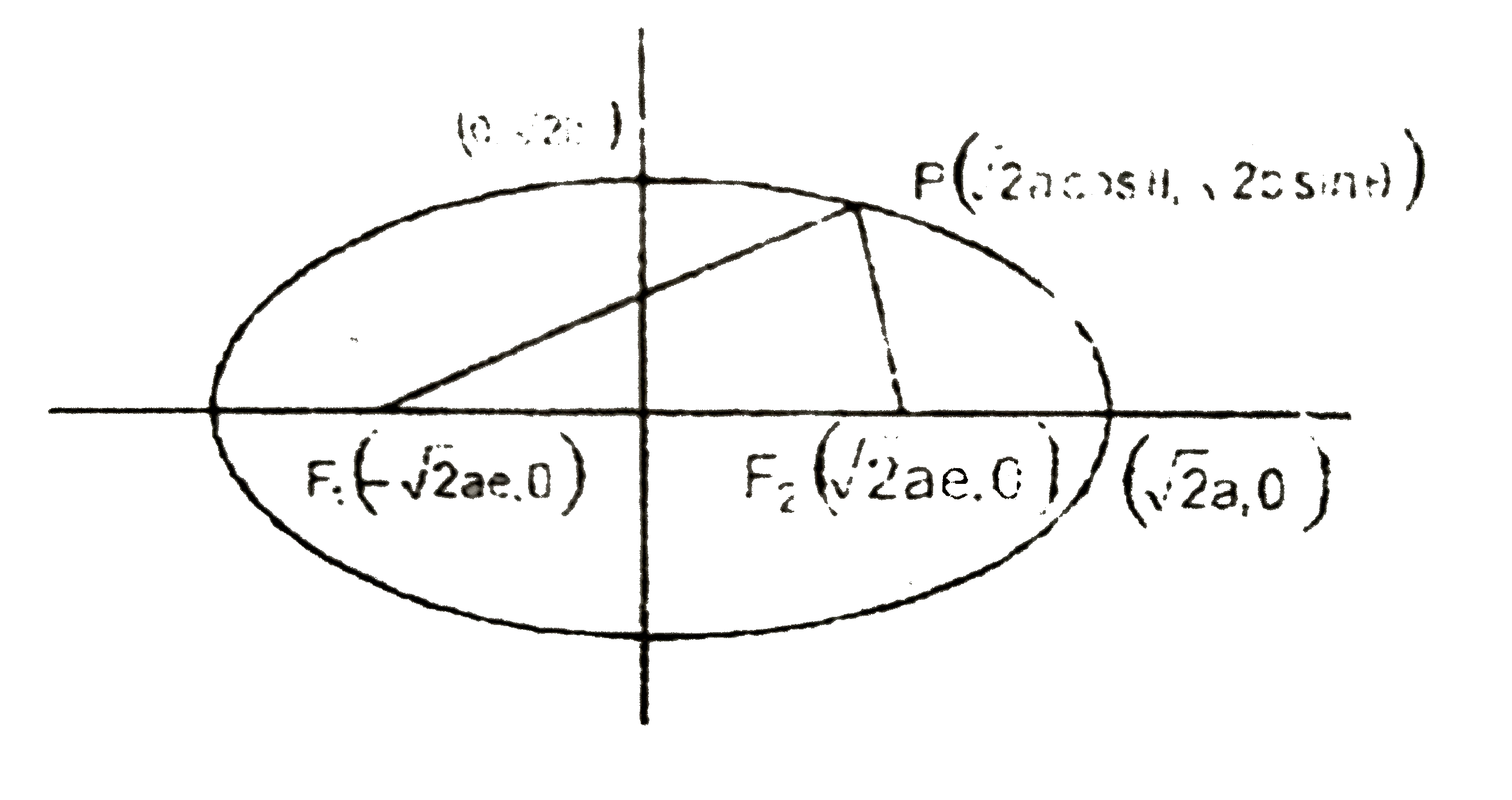
area of
Topper's Solved these Questions
Similar Questions
P is a variable point on the ellipse x2a2+y2b2=2 (a>b) whose foci are F1 and F2. The maximum area (in unit2)of the ΔPFF' is
View SolutionLet S and S'' be the fociof the ellipse x2a2+y2b2=1 whose eccentricity is i.e. P is a variable point on the ellipse. Consider the locus the incenter of ΔPSS''
The eccentricity of the locus oc the P is
View Solution
Knowledge Check
Let P be a variable on the ellipse x225+y216=1 with foci at F1andF2
AArea of △PF1F2 is 12sinθBArea of triantg≤PF1F2 is maximum when θ=π2CCo-ordinate of P are (0, 4)DCentre of the ellipse is (1, 2)The area of the ellipse x2a2+y2b2=1 is
AπabBπ(a2+b2)/4Cπ(a+b)DNoneIf P is a point on the ellipse x216+y225=1 whose foci are S and S', then PS+PS'=8.
A6B8C10D12
Foci of the ellipse x2a2+y2b2=1(a<b) are
View SolutionP is a variable point on the ellipse "9x2+16y2=144" with foci S and S′.Then maximum area of the triangle "SS'P" is
View SolutionLet P be a variable point on the ellipse x2a2+y2b2=1 with foci F1 and F2. If A is the area of the △PF1F2, then the maximum value of A is
View SolutionLet P be a variable point on the elipse x2a2+y2b2=1 with foci F1andF2. If A is the area of the triangle PF1F2, then maximum value of A is
View SolutionLet P be a variable point on the elipse x2a2+y2b2=1 with foci F1andF2. If A is the area of the triangle PF1F2, then maximum value of A is
View Solution