If a,b,c are distinct odd integers and ω is non real cube root of unity, then minimum value of ∣∣aω2+b+cω∣∣, is
A
0
B
3
C
1
D
2√3
Video Solution
Text Solution
The correct Answer is:D
∣∣aω2+b+cω∣∣2
=12((a−b)2+(b−c)2+(c−a)2)
≥12(4+4+5)=12
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
If a,b,c are distinct integers and ω(≠1) is a cube root of unity, then the minimum value of ∣∣a+bω+cω2∣∣+∣∣a+bω2+cω∣∣ is
A2√3B3C4√2D2If a,b,c are distinct integers and ω(≠1) is a cube root of unity, then the minimum value of ∣∣a+bω+cω2∣∣+∣∣a+bω2+cω∣∣ is
A2B3C4√2D6√2If ω is a cube root of unity, then find the value of the following: (1+ω−ω2)(1−ω+ω2)
A1B0C2D4
If a, b, c are distinct integers and a cube root of unity then minimum value of x=∣∣a+bω+cω2∣∣+∣∣a+bω2+cω∣∣
View SolutionIf a, b, c are distanct integers and w≠1 is a cube root of unity, then
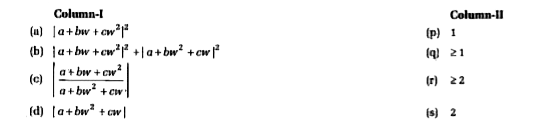
View SolutionIf i=√−1andω is a non-real cube root of unity, then the value of ∣∣ ∣ ∣∣1−ωi−1ωω−ω21+iω2ω2−1i1∣∣ ∣ ∣∣ is
View SolutionIf a,b,c are integers not all equal and w is a cube root of unity (w≠1), then the minimum value of ∣∣a+bw+cw2∣∣ is
View Solution. If a b, and c are integers not all equal andω is a cube root of unity (where ω≠1), then minimum value of ∣∣a+bω+cω2∣∣2 is equal to
View Solution
