Let O be an interior point of ΔABC such that ¯¯¯¯¯¯OA+2¯¯¯¯¯¯OB+3¯¯¯¯¯¯OC=0. Then the ratio of a ΔABC to area of ΔAOC is
The correct Answer is:3
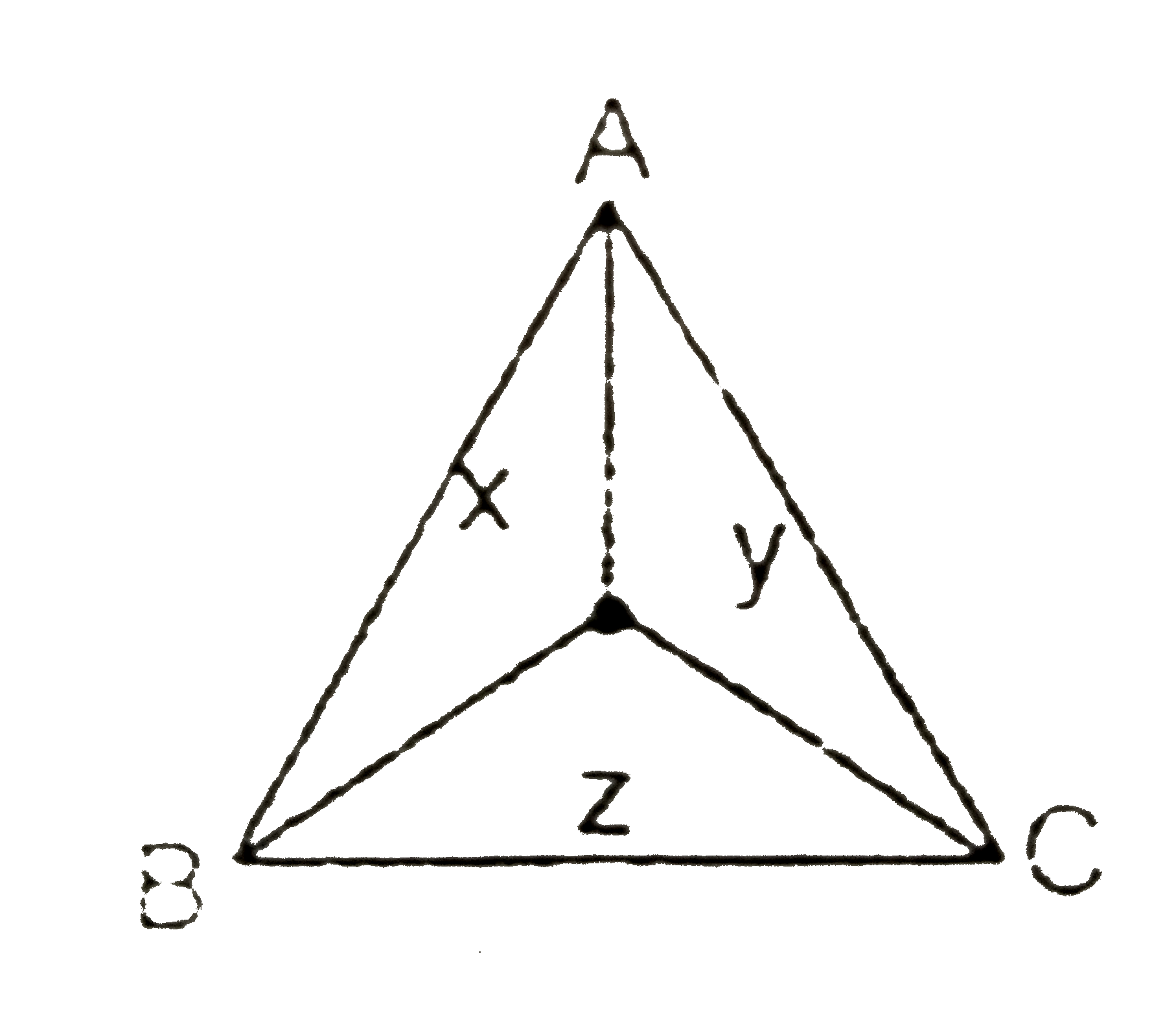
¯¯¯¯¯¯OA+¯¯¯¯¯¯¯¯2OB+¯¯¯¯¯¯¯¯3OC=→0………i
Let x,y,z be the area of triangle OAB,OBC and OCA respectively and area (ΔABC)=A
⇒x+y+z=A………..ii
Taking cross product with ¯¯¯¯¯¯OA on the both sides i and then take modulus on both sides, we get xy=32⇒x=32y
similarly xz=3 and yz=2⇒z=y2
∴ from ii y(32+1+12)=A⇒Ay=3
Topper's Solved these Questions
Similar Questions
Let O be an interior point of ΔABC such that ¯¯¯¯¯¯¯¯2OA+¯¯¯¯¯¯¯¯5OB+¯¯¯¯¯¯¯¯¯¯10OC=¯0. If the ratio of the area of ΔABC to the area of ΔAOC is t, where 'O' is the origin. Find [t].(where [ ] denotes greatest integer function)
View SolutionLet O be an interior point of ΔABC such that 2→OA+5→OB+10→OC=→0
View Solution
Knowledge Check
Let O be an interior point of triangle ABC, such that 2−−→OA+3−−→OB+4−−→OC=0, then the ratio of the area of ΔABC to the area of ΔAOC is
A3:1B3:2C2:1D4:3If P is a point on the plane of ΔABC such that ¯¯¯¯¯¯PA+¯¯¯¯¯¯PB+¯¯¯¯¯¯PC=0, then, for Δ ABC, the point P is
AcircumcentreBcentroidCorthocentreDincentreIf D is the mid -point of side AB of ΔABC, then ¯¯¯¯¯¯AB+¯¯¯¯¯¯BC+¯¯¯¯¯¯AC=
A2(¯¯¯¯¯¯AD−¯¯¯¯¯¯BD)B2(¯¯¯¯¯¯DC−¯¯¯¯¯¯BD)C2(¯¯¯¯¯¯BD−¯¯¯¯¯¯CA)D2(¯¯¯¯¯¯BD−¯¯¯¯¯¯AC)
Let O be an interior point of ΔABC satisfying
−−→OA+2−−→OB+3−−→OC=→0, then the ratio of the areas of ΔABC to ΔAOC is
View SolutionLet O(O being the origin) be n interior point of ΔABC such that →OA+2→OB+3→OC=0. If Δ,Δ1,Δ2andΔ3 are area of ΔABC,ΔOAB,ΔOBC,ΔOCA respectively then
View SolutionLet O be any point in the interior of ΔABC, prove that :
AB+BC+CA<2(OA+OB+OC)
View SolutionIf AD , BE and CF are medians of ΔABC, then ¯¯¯¯¯¯AD+¯¯¯¯¯¯BE+¯¯¯¯¯¯CF =
View SolutionLet G be the centroid of a triangle ABC and O be any other point, then ¯¯¯¯¯¯OA+¯¯¯¯¯¯OB+¯¯¯¯¯¯OC is equal to
View Solution

