One of the diameters of circle circumscribing the rectangle ABCD is4y=x+7. If A and B are the points (−3,4) and (5,4) respectively and area of rectangle is p then p4 is equal to
The correct Answer is:8
Let center is E(α,β)
mid point of AB is Q(1,4)
mOE=β−4α−1=∞ 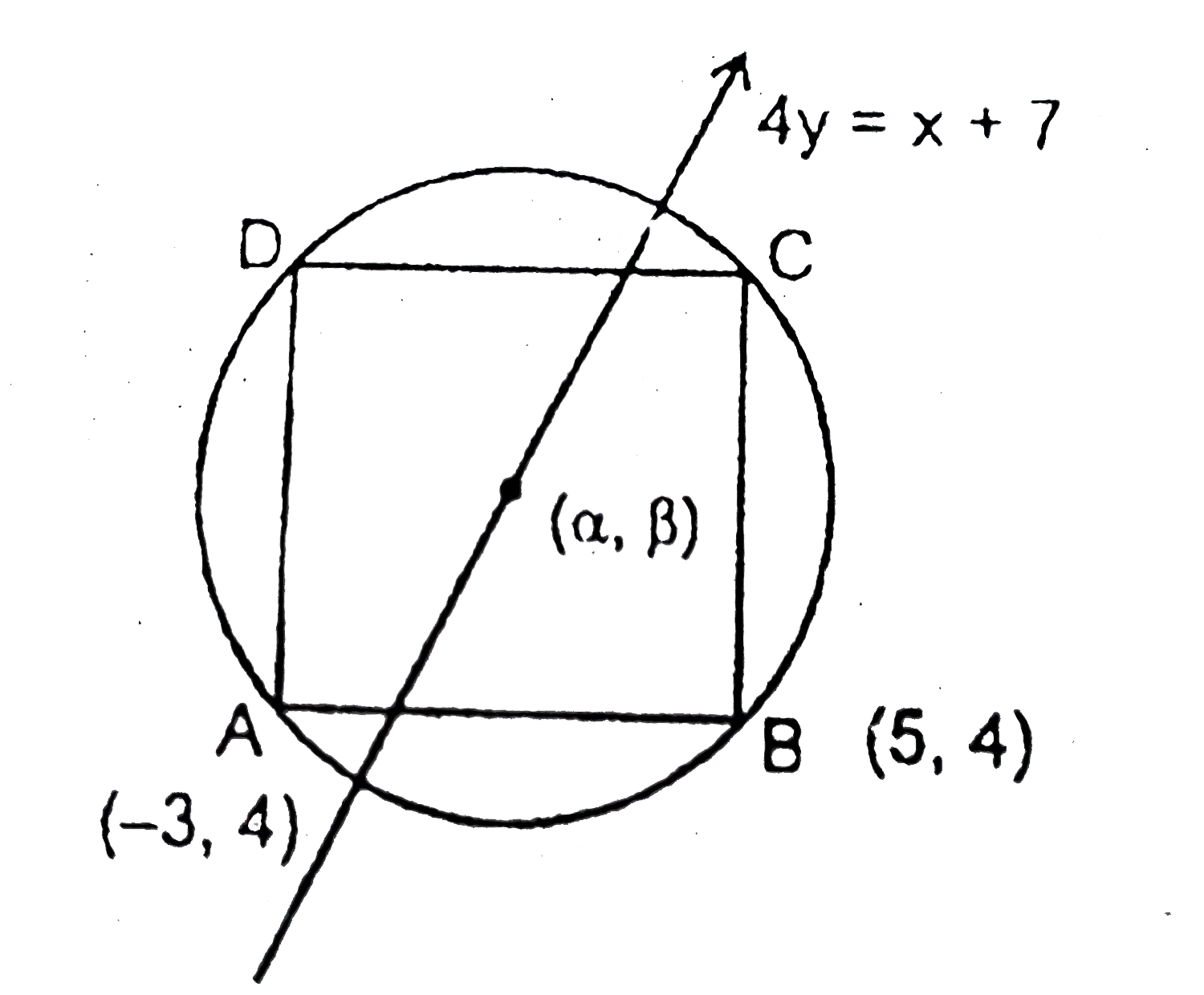
⇒α=1
and 4β=α+7⇒β=2
so E(1,2)
so EQ=2
so area =8×4=32=p
Topper's Solved these Questions
Similar Questions
One of the diameter of a circle circumscribing the rectangle ABCD is 4y=x+7, If A and B are the points (−3,4) and (5,4) respectively, then the area of rectangle is
View SolutionOne of the diameters of the circle circumscribing the rectangle ABCD is 4y = x + 7. If A and B are the points (−3,4)and(5,4) respectively, then find the area of the rectangle.
View Solution
Knowledge Check
In a rectangle ABCD, P,Q are the mid-points of BC and AD respectively and R is any point on PQ, then ΔARB equals :
A12(□ABCD)B13(□ABCD)C14(□ABCD)Dnone of these
One of the diameters of the circle circumscribing the rectangle ABCD is 4y=x+y. If AandB are the points (−3,4)and(5,4) respectively, find the area of the rectangle and equation of the circle.
View SolutionOne of the diameters of the circle circumscribing the rectangle ABCD is 4y=x+7. If AandB are the points (−3,4)and(5,4) and slope of the curve y=axb−x at point (1,1) be 2, then centre of circle is : (A) (a,b) (B) (b,a) (C) (−a,−b) (D) (a,−b)
View Solution2x−y+4=0 is a diameter of a circle which circumscribes a rectangle ABCD. If the coordinates of A, B are (4, 6) and (1, 9) respectively, find the area of this rectangle ABCD.
View SolutionA rectangle ABCD is inscribed in a circle with a diameter lying along the line 3y=x+10. If A and B are the points (−6,7)and(4,7) respectively, find the area of the rectangle and equation of the circle.
View SolutionProve that the centre of the circle circumscribing the cyclic rectangle ABCD is the point of intersection of its diagonals.
View SolutionFind the equation of the circle circumscribing the rectangle whose sides are : x=4,x=−5,y=5,y=−3
View SolutionFind the equation of the circle circumscribing the rectangle whose sides are : x=6,x=−3,y=3,y=−1
View Solution