If (a,b) and (c,d) are two points on the whose equation is y=mx+k, then the distance between (a,b) and (c,d) in terms of a,c and m is
|a+c|√1+m2
|a−c|√1+m2
|a−c|√1+m2
|a−c|(a+m2)
The correct Answer is:B
Let m=tanθ
then equation of line through (a,b) is
x−acosθ=y−bsinθ=r
if (c,d) lies on it at r distance then
⇒c−a=rcosθ⇒r−(c−a)secθ
⇒r=|c−a|√1+m2
Alter: Since (a,b) and (c,d) are on the same line y=mx+k, they satisfy the same equation. Therefore b=ma+kd=mc+k.
Now the distance between (a,b) and (c,d) is
√(a−c)2+(b−d)2
From the first to equations we obtain (b−d)=m(a−c), so that
√(a−c)2+(b−d)2=√(a−c)2+m2(a−c)2
=|a−c|√1+m2
Note we are using the fact that =√x2=|x| for all real x.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The distance between the lines y=mx+c1 and y=mx+c2 is
Ac1−c2√m2+1B|(c1−c2)|√1+m2Cc2−c1√1+m2D0If the points (a,b),(c,d) and (a-c,b-d) are collinear, then
Aab=cdBac=bdCad=bcDNone
if m and b are real numbers and mb>0, then the line whose equation is y=mx+b cannot contain the point
View SolutionThe genes A,B,C and d are located on the same chromosome in such a way that the distance between A and B is 7 map units, between B an C is 2 map is unit, between C and D is. 4.5 units. What is the distance between A and D? What is the porbability of linkage between B and D and between A and D?
View SolutionIn a class room 4 friends are seated at the point A,B,C,D as shown in figure.
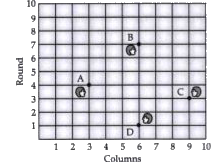
Find the distance between B and C.
View SolutionIn a class room 4 friends are seated at the point A,B,C,D as shown in figure.
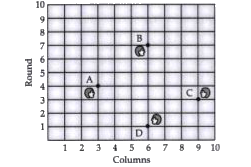
Find the distance between A and D.
View SolutionIf c,d are the roots of the equation (x−a)(x−b)−k=0 , prove that a, b are roots of the equation (x−c)(x−d)+k=0.
View SolutionAB and CD are two chords of a circle such that AB = 6 cm, CD = 12 cm and AB || CD. If the distance between AB and CD is 3 cm, find the radius of the circle
View Solution
