How many pair (s) of geometrical isomers are possible with C6H12(only in open chain structures)
The correct Answer is:[4]
To determine the number of pairs of geometrical isomers possible for the compound with the formula C6H12 in open-chain structures, we can follow these steps:
Step 1: Understand the Structure
The molecular formula C6H12 indicates that the compound is an alkene (due to the presence of double bonds) or a cycloalkane. However, since we are only considering open-chain structures, we will focus on alkenes.
Step 2: Identify the Degree of Unsaturation
The degree of unsaturation can be calculated using the formula:
Degree of Unsaturation=(2n+2−m)2
where n is the number of carbons and m is the number of hydrogens. For C6H12:
Degree of Unsaturation=(2×6+2−12)2=(12−12)2=0
This means we can have one or more double bonds in the structure.
Step 3: Determine Possible Structures
To create geometrical isomers, we need to have at least one double bond between carbon atoms. The configurations around the double bond can lead to cis and trans isomers.
Step 4: Identify Positions for Double Bonds
1. Single Double Bond:
- If we place a double bond between C1 and C2, we can have cis and trans isomers.
- If we place a double bond between C2 and C3, we can have another pair of cis and trans isomers.
- If we place a double bond between C3 and C4, we can have another pair of cis and trans isomers.
- If we place a double bond between C4 and C5, we can have another pair of cis and trans isomers.
2. Multiple Double Bonds:
- If we consider placing two double bonds, we can also create different configurations leading to more isomers.
Step 5: Count the Pairs of Geometrical Isomers
After analyzing the possible positions of the double bonds:
- C1=C2: 1 pair (cis and trans)
- C2=C3: 1 pair (cis and trans)
- C3=C4: 1 pair (cis and trans)
- C4=C5: 1 pair (cis and trans)
Thus, we can have a total of 4 pairs of geometrical isomers.
Final Answer
The total number of pairs of geometrical isomers possible with C6H12 in open-chain structures is 4 pairs.
---
The molecular formula C6H12 indicates that the compound is an alkene (due to the presence of double bonds) or a cycloalkane. However, since we are only considering open-chain structures, we will focus on alkenes.
The degree of unsaturation can be calculated using the formula:
Degree of Unsaturation=(2n+2−m)2
where n is the number of carbons and m is the number of hydrogens. For C6H12:
Degree of Unsaturation=(2×6+2−12)2=(12−12)2=0
This means we can have one or more double bonds in the structure.
To create geometrical isomers, we need to have at least one double bond between carbon atoms. The configurations around the double bond can lead to cis and trans isomers.
1. Single Double Bond:
- If we place a double bond between C1 and C2, we can have cis and trans isomers.
- If we place a double bond between C2 and C3, we can have another pair of cis and trans isomers.
- If we place a double bond between C3 and C4, we can have another pair of cis and trans isomers.
- If we place a double bond between C4 and C5, we can have another pair of cis and trans isomers.
- If we consider placing two double bonds, we can also create different configurations leading to more isomers.
After analyzing the possible positions of the double bonds:
- C1=C2: 1 pair (cis and trans)
- C2=C3: 1 pair (cis and trans)
- C3=C4: 1 pair (cis and trans)
- C4=C5: 1 pair (cis and trans)
The total number of pairs of geometrical isomers possible with C6H12 in open-chain structures is 4 pairs.
Topper's Solved these Questions
Similar Questions
Knowledge Check
How many geometrical isomers are possible for
 A2B3C4D8
A2B3C4D8How many pairs of chain isomers are possible for C4H16Cl?
A4B3C2D1how many structural isomers are possible for C6H14?
A4B5C6D7
How many geometrical isomers are possible for
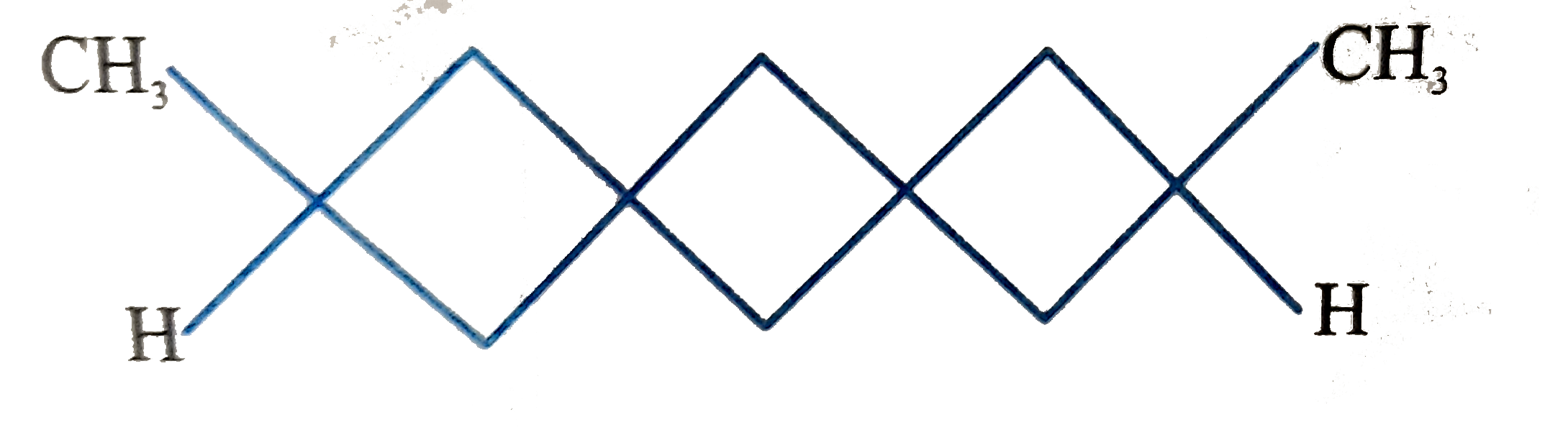
View SolutionHow many geometrical isomers are possible for the [Ni(NH3)4]2+?
View SolutionHow many structural isomers are possible for C6H14 ?
View SolutionHow many optical isomers are possible for C5H11Cl?
View SolutionHow many structural isomers are possible by C4H9Br
View Solution


