How many geometrical isomers are possible for the [Ni(NH3)4]2+?
To determine how many geometrical isomers are possible for the complex (Ni(NH3)4)2+, we can follow these steps:
Step 1: Determine the oxidation state of Nickel (Ni)
The complex (Ni(NH3)4)2+ indicates that Nickel is in the +2 oxidation state. This is because the ammonia (NH3) ligands are neutral.
Hint: Check the charge of the complex and the nature of the ligands to find the oxidation state.
Step 2: Identify the coordination number and geometry
In this complex, Nickel is coordinated to four ammonia molecules (NH3). The coordination number is 4, and for a coordination number of 4, the common geometries are tetrahedral and square planar. However, since NH3 is a strong field ligand, it typically leads to a tetrahedral geometry in this case.
Hint: Recall the common geometries associated with different coordination numbers.
Step 3: Analyze the possibility of geometrical isomers
Geometrical isomers arise when there are different spatial arrangements of the ligands around the central metal atom. In tetrahedral complexes, the ligands can be arranged in different ways, but they do not form cis or trans isomers like square planar complexes do. In tetrahedral complexes, all arrangements are considered equivalent due to symmetrical properties.
Hint: Remember that geometrical isomers typically involve cis and trans arrangements, which are not applicable in tetrahedral structures.
Step 4: Conclusion
Since (Ni(NH3)4)2+ has a tetrahedral geometry and does not allow for cis or trans arrangements, there are no geometrical isomers possible for this complex.
Final Answer: The number of geometrical isomers for (Ni(NH3)4)2+ is 0.
The complex (Ni(NH3)4)2+ indicates that Nickel is in the +2 oxidation state. This is because the ammonia (NH3) ligands are neutral.
In this complex, Nickel is coordinated to four ammonia molecules (NH3). The coordination number is 4, and for a coordination number of 4, the common geometries are tetrahedral and square planar. However, since NH3 is a strong field ligand, it typically leads to a tetrahedral geometry in this case.
Geometrical isomers arise when there are different spatial arrangements of the ligands around the central metal atom. In tetrahedral complexes, the ligands can be arranged in different ways, but they do not form cis or trans isomers like square planar complexes do. In tetrahedral complexes, all arrangements are considered equivalent due to symmetrical properties.
Since (Ni(NH3)4)2+ has a tetrahedral geometry and does not allow for cis or trans arrangements, there are no geometrical isomers possible for this complex.
Topper's Solved these Questions
- COORDINATION COMPOUNDSBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - COORDINATION COMPOUNDSEXERCISE - SHORT ANSWER-I TYPE QUESTIONS
18 Videos
- COORDINATION COMPOUNDSBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - COORDINATION COMPOUNDSEXERCISE - SHORT ANSWER-II TYPE QUESTIONS
8 Videos
- COORDINATION COMPOUNDSBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - COORDINATION COMPOUNDSEXERCISE - LONG ANSWER TYPE QUESTIONS
3 Videos
- CHEMISTRY IN EVERYDAY LIFEBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CHEMISTRY IN EVERYDAY LIFEEXERCISE - LONG ANSWER TYPE QUESTIONS
2 Videos
- ELECTROCHEMISTRY BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTROCHEMISTRY EXERCISE - LONG ANSWER TYPE QUESTIONS (5 Marks)
7 Videos
Similar Questions
Knowledge Check
How many geometrical isomers are possible for complex [Mab(AB)2]n±?
A5B4C3D6How many geometrical isomers are possible for complex [Mab(AB)2]n±?
A5B4C3D6
How many geometrical isomers are possible for the complex ion [Cr(NH3)(OH)2CI3]2−.
View SolutionHow many geometrical isomers are possible for MA2B2C2 ?
View SolutionHow many type of geometrical isomers are possible for [M(NH3)BrCl(H2O)], where M is Pt+2 ?
View SolutionHow many geometrical isomers arepossible for [Pt(NO2)(NH2OH)(Py)]+?
View Solution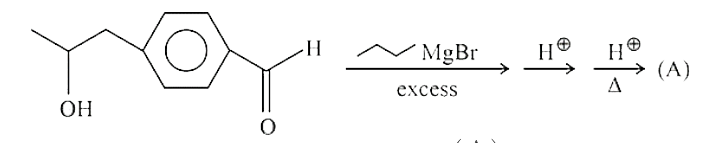
How many geometrical isomer of (A) is possible?
View Solution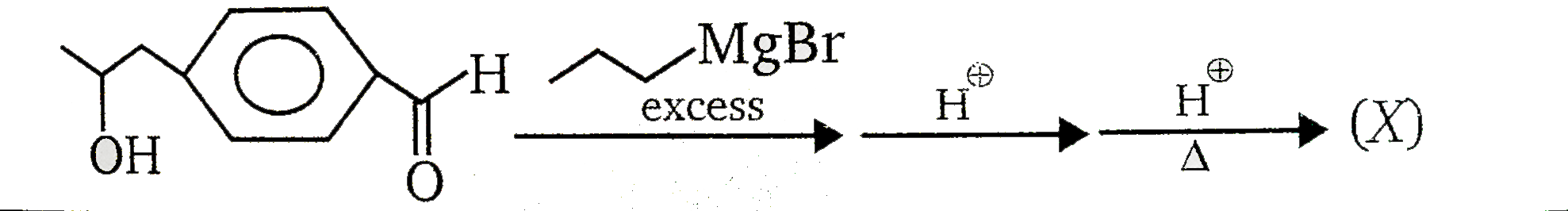
How many geometrical isomer of (X) is possible ?
View Solution
