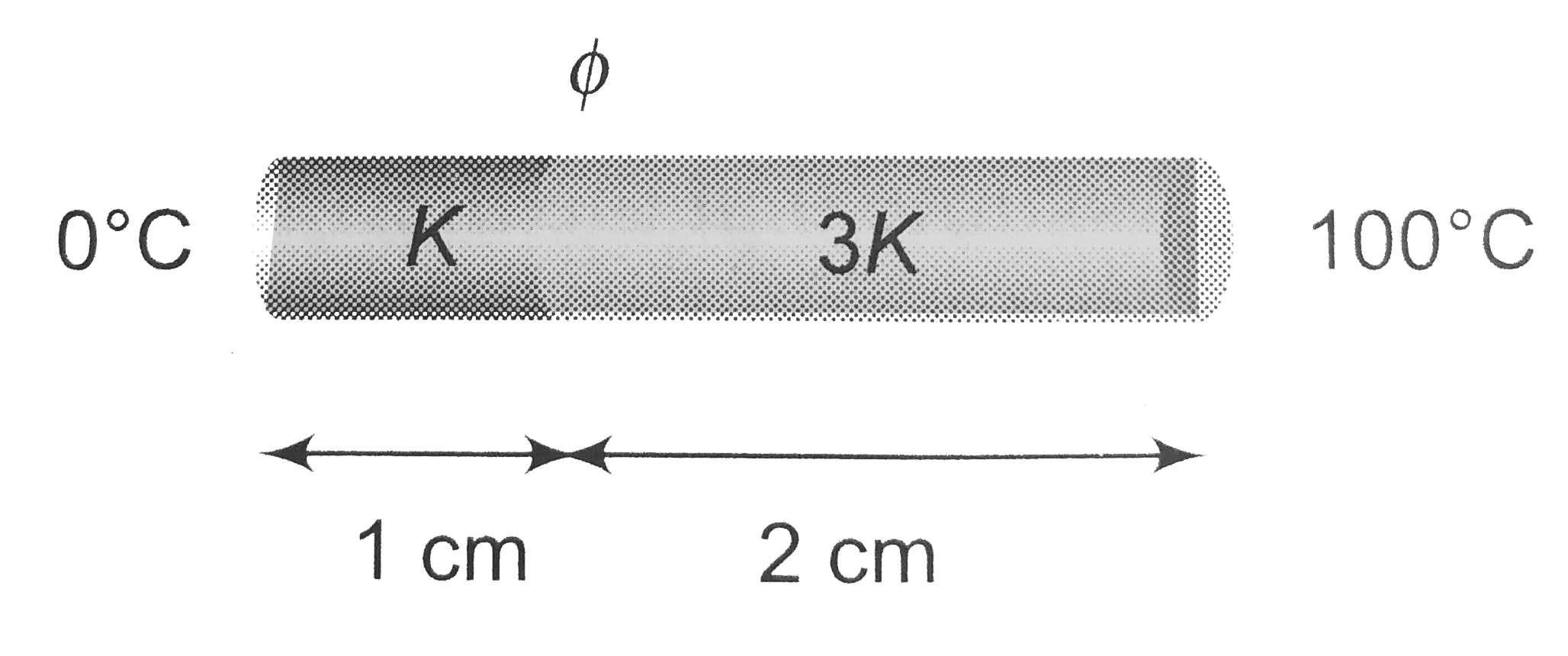
Two bars of thermal conductivities and and lengths and respectively have equal cross-sectional area, they are joined lengths wise as shown in the figure. If the temperature at the ends of this composite br is and respectively (see figure), then the temperature of the interface is
The correct Answer is:C
Step by step video, text & image solution for Two bars of thermal conductivities K and 3K and lengths 1 cm and 2 cm respectively have equal cross-sectional area, they are joined lengths wise as shown in the figure. If the temperature at the ends of this composite br is 0^(@)C and K^(2)//l respectively (see figure), then the temperature phi of the interface is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ERRORLESS CHAPTER - TRANSMISSION OF HEATEXERCISE - Convection13videos
TRANSMISSION OF HEAT
- BOOK - ERRORLESS CHAPTER - TRANSMISSION OF HEATEXERCISE - Radiation (General, Kirchoff s law, Black body)38videos
TRANSMISSION OF HEAT
- BOOK - ERRORLESS CHAPTER - THERMOMETRY, THERMAL EXPANSION AND CALORIMETRY EXERCISE - Self Evaluation Test15videos
THERMOMETRY, THERMAL EXPANSION AND CALORIMETRY
- BOOK - ERRORLESS CHAPTER - UNITS, DIMENSION & MEASUREMENTSEXERCISE - All Questions333videos
UNITS, DIMENSION & MEASUREMENTS
Similar Questions
Two materials having coefficients of thermal conductivity ‘3 K’ and ‘K’ and thickness ‘d’ and ‘3 d’, respectively, are joined to form a slab as shown in the figure. The temperatures of the outer surfaces are θ2 and θ1 respectively, (θ2>θ1) The temperature at the interface is:
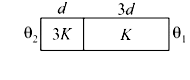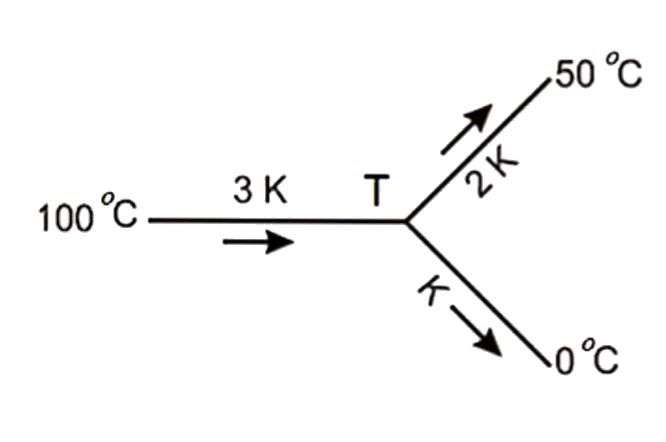
View SolutionThree rods of the same dimension have thermal conductivity 3K, 2K and K as shown in the figure. The temperature of the junction in steady-state is
View Solution
Knowledge Check
- Question 1 - Select One
Two rods having thermal conductivity in the ratio of 5 : 3 having equal lengths and equal cross-sectional area are joined by face to face. If the temperature of the free end of the first rod is 100∘C and free end of the second rod is 20∘C . Then temperature of the junction is
A70∘CB50∘CC50∘CD90∘C - Question 2 - Select One
Three rods A, B and C of the same length and same cross-sectional area are joined as shown. Their thermal conductivities are in the ratio 1:2:3/2. If the open ends of A and C are at 200∘C and 18∘C, respectively, then the temperature at the junction of A at steady state is
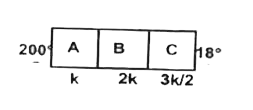A156∘CB148∘CC116∘CD74∘C - Question 3 - Select One
Two rods of similar area of cross section and length are joined as shown in the figure. The ratio of their thermal conductivity is 2:3. The free ends are maintained at 100∘C and 0∘C respectivley. THE temperature at junction in steady state is
A50∘CB40∘CC60∘D80∘C
Three bars of equal lengths and equal area of cross-section are connected in series fig. their thermal conducitives are in the ratio 2:3:4. If at the steady state the open ends of the first and the last bars are at temperature 200∘C and 20∘C respectively, find the temperature of both the junctions.
.View SolutionTwo rods of length l and 2l thermal conductivities 2K and K are connected end to end. If cross sectional areas of two rods are eual, then equivalent thermal conductivity of the system is .
View SolutionThree rods of the same dimension have thermal conductivity 3K, 2K and K as shown in the figure. The temperature of the junction in steady-state is
View Solution_2019_CBT4_E01_064_Q01.png)
Two conductors of same cross-section and conductivities K, 3K and length 3 d and d respectively are connected end to end as shown in figure. Temperature of end of first conductor is θ1 and that of second conductor is θ2 .the temperature of junction is steady state is (θ2>θ1)View SolutionMetal rods X and Y of identical cross-sectional area, have lengths 60 cm and 30 cm respectively. They are made of metals of thermal conductivities λx and λy. They are well-lagged and joined end-to-end as shown in the figure-4.43. One end of X is maintained at 100∘C and the opposite end of Y is maintained at 0∘C. When steady conditions have been .reached, the temperature of the junction is found to be 25∘C.
What is the value of λxλy ?
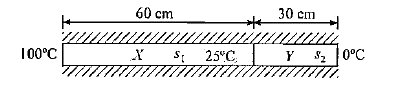View Solution