A rocket is launched with velocity 10 km / s . If radius of earth is R , then maximum height attained by it will be
2 R
3 R
4 R
5 R
The correct Answer is:C
To find the maximum height attained by a rocket launched with a velocity of 10 km/s from the surface of the Earth, we can use the principle of conservation of energy. Here’s a step-by-step solution:
Step 1: Understand the Initial Conditions
The rocket is launched from the surface of the Earth with an initial velocity v0=10km/s. The radius of the Earth is denoted as R.
Step 2: Write the Conservation of Energy Equation
At the surface of the Earth, the total mechanical energy (kinetic + potential) can be expressed as:
Einitial=KE+PE=12mv20−GMmR
Where:
- KE=12mv20 is the kinetic energy,
- PE=−GMmR is the gravitational potential energy (negative because it is defined relative to infinity).
At the maximum height h, the velocity of the rocket becomes zero, so the total mechanical energy is:
Efinal=PE=−GMmR+h
Step 3: Set the Initial Energy Equal to the Final Energy
Using conservation of energy:
12mv20−GMmR=−GMmR+h
Step 4: Simplify the Equation
We can cancel m from both sides (assuming m≠0):
12v20−GMR=−GMR+h
Step 5: Rearrange the Equation
Rearranging gives us:
12v20=GMR−GMR+h
12v20=GM(1R−1R+h)
Step 6: Find a Common Denominator
The right-hand side can be simplified:
1R−1R+h=(R+h)−RR(R+h)=hR(R+h)
Thus, we have:
12v20=GM⋅hR(R+h)
Step 7: Solve for h
Rearranging gives:
h=R(R+h)2GMv20
This can be further simplified, but we can also substitute g=GMR2 (acceleration due to gravity at the surface of the Earth):
h=R22gv20−Rh2g
Solving for h leads to:
h(1+12gv20)=R2v202g
h=R2v202g(1+12gv20)
Step 8: Substitute Values
Substituting v0=10×103m/s and g≈9.8m/s2:
h≈R2(104)22×9.8(1+(104)22×9.8)
Step 9: Approximate the Result
After solving, we find that the maximum height h is approximately 4R.
Conclusion
Thus, the maximum height attained by the rocket is approximately 4R.
---
The rocket is launched from the surface of the Earth with an initial velocity v0=10km/s. The radius of the Earth is denoted as R.
At the surface of the Earth, the total mechanical energy (kinetic + potential) can be expressed as:
Einitial=KE+PE=12mv20−GMmR
Where:
- KE=12mv20 is the kinetic energy,
- PE=−GMmR is the gravitational potential energy (negative because it is defined relative to infinity).
Efinal=PE=−GMmR+h
Using conservation of energy:
12mv20−GMmR=−GMmR+h
We can cancel m from both sides (assuming m≠0):
12v20−GMR=−GMR+h
Rearranging gives us:
12v20=GMR−GMR+h
12v20=GM(1R−1R+h)
The right-hand side can be simplified:
1R−1R+h=(R+h)−RR(R+h)=hR(R+h)
Thus, we have:
12v20=GM⋅hR(R+h)
Rearranging gives:
h=R(R+h)2GMv20
This can be further simplified, but we can also substitute g=GMR2 (acceleration due to gravity at the surface of the Earth):
h=R22gv20−Rh2g
Solving for h leads to:
h(1+12gv20)=R2v202g
h=R2v202g(1+12gv20)
Substituting v0=10×103m/s and g≈9.8m/s2:
h≈R2(104)22×9.8(1+(104)22×9.8)
After solving, we find that the maximum height h is approximately 4R.
Thus, the maximum height attained by the rocket is approximately 4R.
Topper's Solved these Questions
- GRAVITATIONBook:ERRORLESS Chapter:GRAVITATIONExercise:Motion of Satellite
Explore 67 Videos
- GRAVITATIONBook:ERRORLESS Chapter:GRAVITATIONExercise:Kepler’s Laws of Planetary Motion
Explore 51 Videos
- GRAVITATIONBook:ERRORLESS Chapter:GRAVITATIONExercise:Acceleration Due to Gravity
Explore 87 Videos
- FRICTIONBook:ERRORLESS Chapter:FRICTIONExercise:MCQ S
Explore 125 Videos
- MOTION IN ONE DIMENSIONBook:ERRORLESS Chapter:MOTION IN ONE DIMENSIONExercise:Motion In One Dimension
Explore 24 Videos
Similar Questions
A body is projected vertically upward from. the surface of the earth.with a velocity equal to half its escape velocity. If R is radius of the earth, then the maximum height attained by the,body is (Rn). Find n.
View SolutionA body is projected vertically upwards from the surface of earth with a velocity equal to half the escape velocity. If R be the radius of earth, maximum height attained by the body from the surface of earth is Rn. Find the value of n.
View Solution
Knowledge Check
A particle is thrown vertically upwards. If its velocity is half of the maximum height is 20m/s, then maximum height attained by it is
A25 mB30 mC35 mD40 mA particle is thrown vertically upward. Its velocity at half of the height is 10 m/s. Then the maximum height attained by it : -
(g=10m/s2)A8 mB20 mC10 mD16 mIf an object is projected vertically upwards with speed , half the escape speed of earth , then the aximum height attained by it is [ R is radius of earth ]
ARBR2C2RDR3
A body is projected vertically upwards from the surface of the earth with a velocity equal to half of escape velocity of the earth. If R is radius of the earth, maximum height attained by the body from the surface of the earth is
View SolutionA particle is projected vertically upwards with a velocity √gR, where R denotes the radius of the earth and g the acceleration due to gravity on the surface of the earth. Then the maximum height ascended by the particle is
View SolutionA rocket is launched upward from the earth surface whose velocity time graph shown in figure. Then maximum height attained by the rocket is :-
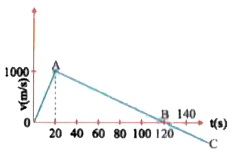
View SolutionA rocket is launched upward from the earth surface whose velocity time graph shown in figure. Then maximum height attained by the rocket is :-

View SolutionA rocket is launched vertical from the surface of the earth of radius R with an initial speed v. If atmospheric resistance is neglected, then maximum height attained by the rocket is
View Solution

