In a gravitational field, at a point where the gravitational potential is zero
The gravitational field is necessarily zero
The gravitational field is not necessarily zero
Nothing can be said definitely about the gravitational field
None of these
The correct Answer is:A
To solve the question regarding the gravitational field at a point where the gravitational potential is zero, we can follow these steps:
Step 1: Understand the relationship between gravitational potential and gravitational field
The gravitational potential (V) at a point in a gravitational field is related to the gravitational field (E) by the equation:
E=−dVdr
This means that the gravitational field is the negative gradient of the gravitational potential.
Step 2: Analyze the condition of zero gravitational potential
If the gravitational potential (V) is zero at a certain point, we need to consider what this implies about the gravitational field (E) at that point.
Step 3: Evaluate the implications of zero potential
If V = 0 at a point, it does not necessarily mean that the gravitational field (E) is also zero. The gravitational field can still have a non-zero value while the potential is zero. For example, the potential can be zero at a point in space where the gravitational field is directed towards a mass.
Step 4: Consider the definition of gravitational potential
Gravitational potential is defined as the work done per unit mass to bring a mass from infinity to that point. Therefore, if we are at a point where the potential is zero, it means that the work done to bring a mass from infinity to that point is zero, but it does not imply that the gravitational field itself is zero.
Step 5: Conclusion
Thus, the statement that "where the gravitational potential is zero, the gravitational field will also be zero" is incorrect. The gravitational field can exist even when the potential is zero.
Final Answer
The gravitational field does not have to be zero at a point where the gravitational potential is zero.
---
The gravitational potential (V) at a point in a gravitational field is related to the gravitational field (E) by the equation:
E=−dVdr
This means that the gravitational field is the negative gradient of the gravitational potential.
If the gravitational potential (V) is zero at a certain point, we need to consider what this implies about the gravitational field (E) at that point.
If V = 0 at a point, it does not necessarily mean that the gravitational field (E) is also zero. The gravitational field can still have a non-zero value while the potential is zero. For example, the potential can be zero at a point in space where the gravitational field is directed towards a mass.
Gravitational potential is defined as the work done per unit mass to bring a mass from infinity to that point. Therefore, if we are at a point where the potential is zero, it means that the work done to bring a mass from infinity to that point is zero, but it does not imply that the gravitational field itself is zero.
Thus, the statement that "where the gravitational potential is zero, the gravitational field will also be zero" is incorrect. The gravitational field can exist even when the potential is zero.
The gravitational field does not have to be zero at a point where the gravitational potential is zero.
Topper's Solved these Questions
- GRAVITATIONBook:ERRORLESS Chapter:GRAVITATIONExercise:Motion of Satellite
Explore 67 Videos
- GRAVITATIONBook:ERRORLESS Chapter:GRAVITATIONExercise:Kepler’s Laws of Planetary Motion
Explore 51 Videos
- GRAVITATIONBook:ERRORLESS Chapter:GRAVITATIONExercise:Acceleration Due to Gravity
Explore 87 Videos
- FRICTIONBook:ERRORLESS Chapter:FRICTIONExercise:MCQ S
Explore 125 Videos
- MOTION IN ONE DIMENSIONBook:ERRORLESS Chapter:MOTION IN ONE DIMENSIONExercise:Motion In One Dimension
Explore 24 Videos
Similar Questions
Where is the gravitational field zero and where is the gravitational potential zero, in case of Earth?
View SolutionFind the gravitational potential at a point where the gravitational field intensity is zero due to two particles of masses m1=1kg and m2=4kg separated through a distance l=3m ?
View Solution
Knowledge Check
In some region, the gravitational field is zero. The gravitational potential in this region
AMust be variableBMust be constantCCannot be zeroDMust be zeroTwo bodies of masses M1 and M2, are placed at a distance R apart. Then at the position where the gravitational field due to them is zero, the gravitational potential is
A−G√M1RB−G√M2RC−(√M1+√M2)2GRD−(√M1−√M2)2GRThe bodies of mass m and 4m are placed at a distance of 6m apart. P is the point on the line joining two bodies where gravitational field is zero. The gravitational potential at this point is
A−32GmB−52GmC−92GmD−72Gm
Explain gravitational potential at a point and gravitational potential energy of a body in a gravitational field. Establish a relation between them.
View SolutionThere are three identical point mass bodies each of mass m locted at the vertices of an equilateral triangle with side r. They are experting gravitational force of attraction on each other, which can be given by Newton's law of gravitaiton. Each mass body produces its gravitational field in the surrounding region. the magnitude of gravitational field at a point due to a point mass body is the measure of gravitaitonal intensity at that point. The gravitational potential at a point in a gravitational field is the amount of workdone in bringing a unit mass body infinity to the given point without acceleration.
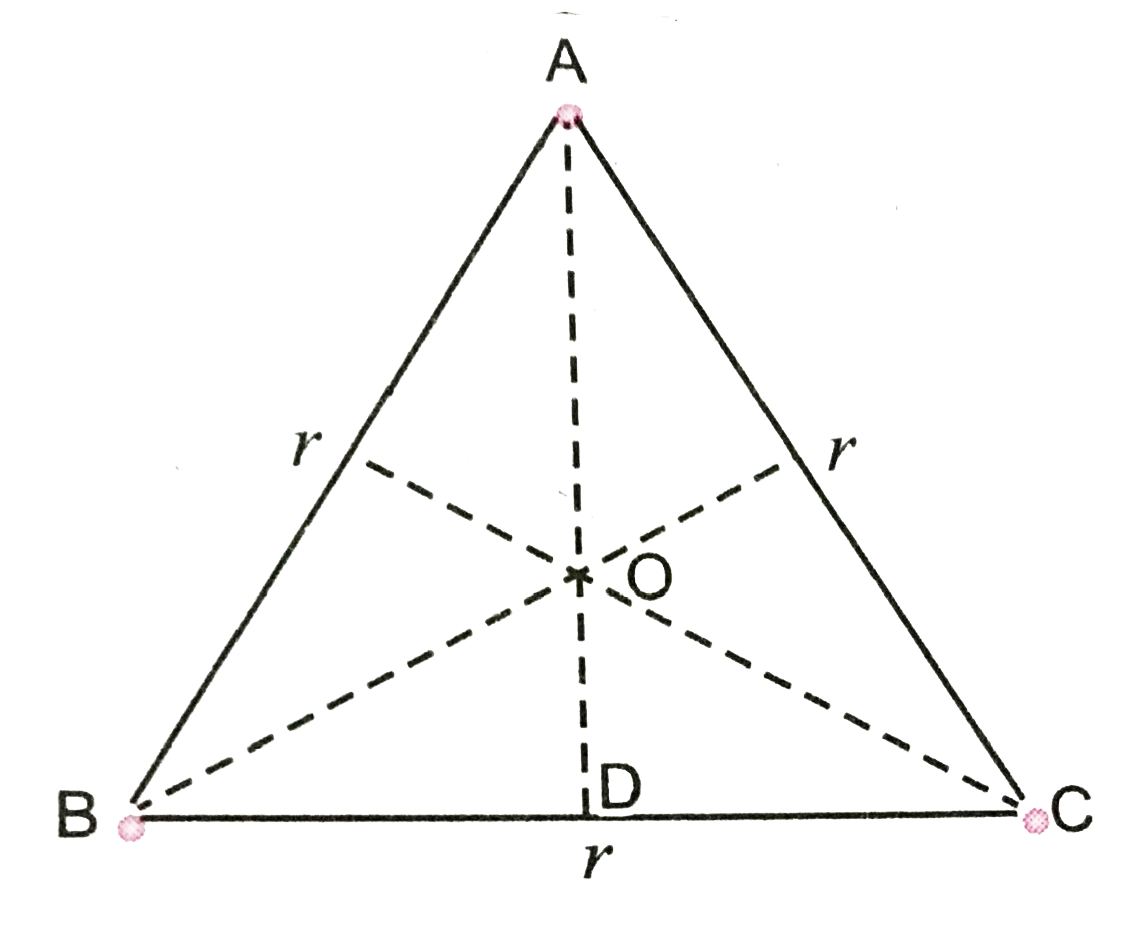
Answer the following questions :
Magnitude of gravitational field at the mid point D of arm BC of triangle ABC is
View SolutionTwo particles of masses 'm' and '9m' are separated by a distance 'r'. At a point on the line joining them the gravitational field is zero. The gravitational potential at that point is (G = Universal constant of gravitation)
View SolutionAssertion : If gravitational potential at some point is zero, then gravitational field strength at that point will also be zero.
Reason : Except at infinity gravitational potential due to a system of point masses at some finite distance can't be zero.
View SolutionTwo bodies of masses m and M are placed at distance d apart. The gravitational potential (V) at the position where the gravitational field due to them is zero V is
View Solution