Which of the following graph depicts spring constant k versus length l of the spring correctly
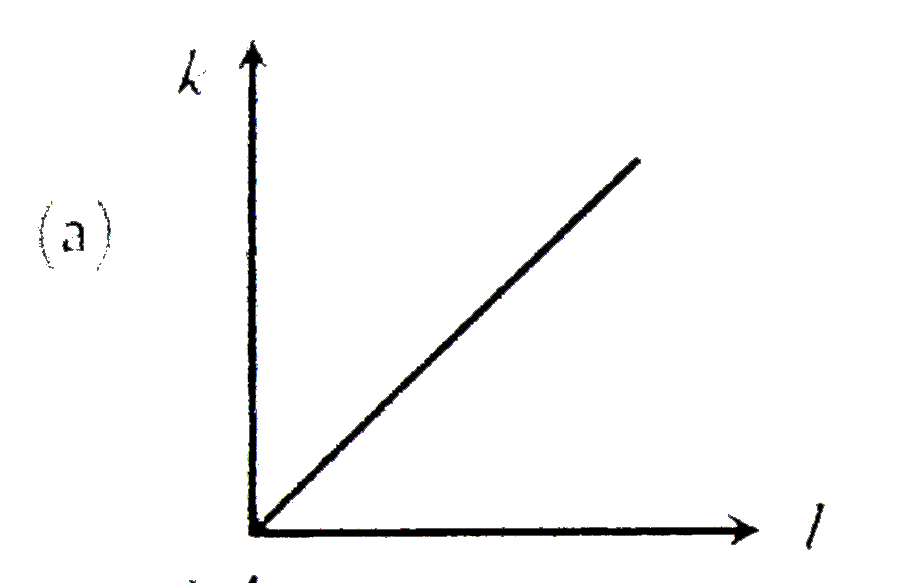
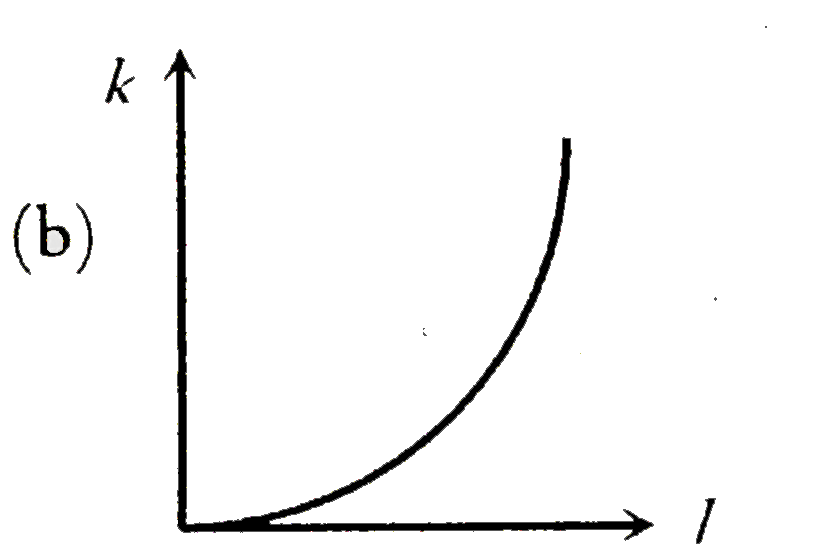
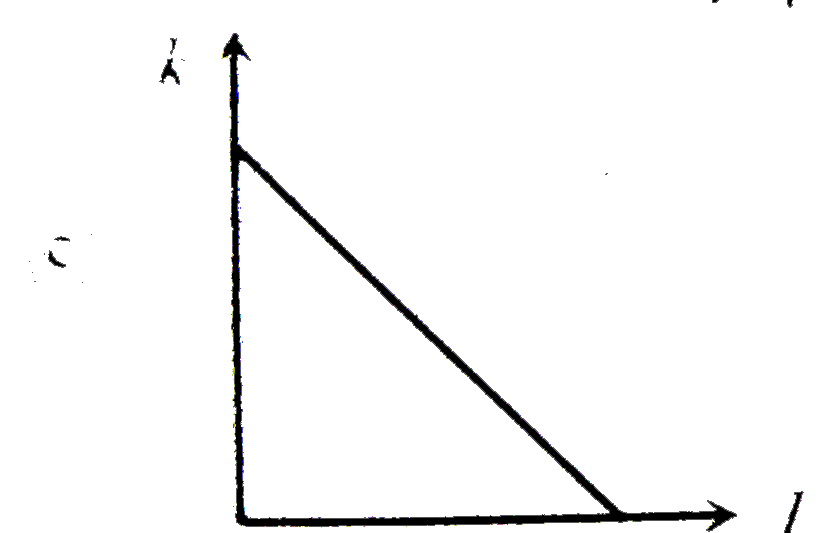
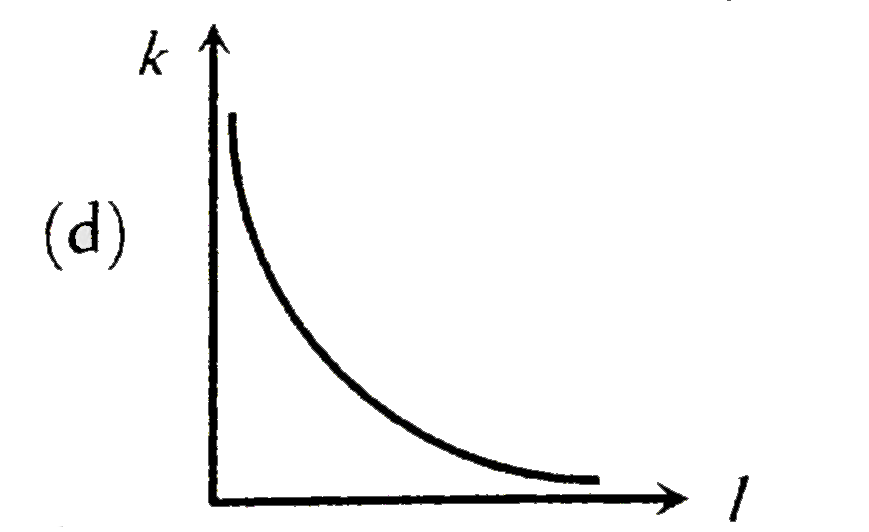
The correct Answer is:D
To solve the problem of determining which graph depicts the relationship between the spring constant k and the length l of the spring, we can follow these steps:
Step 1: Understand the relationship between force, spring constant, and displacement
The spring force can be described by Hooke's Law, which states:
F=−kx
where F is the force applied, k is the spring constant, and x is the displacement from the equilibrium position.
Step 2: Rearranging the equation
When we consider the magnitude of the force, we can write:
F=kx
From this, we can express the spring constant k in terms of the force F and the displacement x:
k=Fx
Step 3: Analyzing the effect of length on the spring constant
If we keep the force F constant and increase the displacement x (which corresponds to the length l of the spring), the spring constant k will change. Specifically, since k is inversely proportional to x:
k∝1x
This means that as the length l (or displacement x) increases, the value of k decreases.
Step 4: Graphical representation
The relationship k∝1l indicates that if we were to plot k against l, we would expect a hyperbolic curve that decreases as l increases. Therefore, the graph depicting k versus l should show a downward trend, indicating that as the length of the spring increases, the spring constant decreases.
Conclusion
Based on the analysis, the correct graph that depicts the relationship between the spring constant k and the length l of the spring is a graph that shows k decreasing non-linearly as l increases.
The spring force can be described by Hooke's Law, which states:
F=−kx
where F is the force applied, k is the spring constant, and x is the displacement from the equilibrium position.
When we consider the magnitude of the force, we can write:
F=kx
From this, we can express the spring constant k in terms of the force F and the displacement x:
k=Fx
If we keep the force F constant and increase the displacement x (which corresponds to the length l of the spring), the spring constant k will change. Specifically, since k is inversely proportional to x:
k∝1x
This means that as the length l (or displacement x) increases, the value of k decreases.
The relationship k∝1l indicates that if we were to plot k against l, we would expect a hyperbolic curve that decreases as l increases. Therefore, the graph depicting k versus l should show a downward trend, indicating that as the length of the spring increases, the spring constant decreases.
Based on the analysis, the correct graph that depicts the relationship between the spring constant k and the length l of the spring is a graph that shows k decreasing non-linearly as l increases.
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - ERRORLESS CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Assertion & Reason
25 Videos
- NEWTONS LAWS OF MOTIONBOOK - ERRORLESS CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Self Evaluation Test
16 Videos
- NEWTONS LAWS OF MOTIONBOOK - ERRORLESS CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Critical Thinking
19 Videos
- MOTION IN TWO DIMENSIONBOOK - ERRORLESS CHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Exercise
319 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on motion of connected mass)
10 Videos
Similar Questions
Knowledge Check
The electrical analog of a spring constant k is
ALBRCCD1CA block of mass 'm' is attached to a spring in natural length of spring constant 'k'. The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.
 A14√mv2kB√mv2kC12√mv2kD2√mv2k
A14√mv2kB√mv2kC12√mv2kD2√mv2kThe spring constant of spring A is twice the spring constant of spring B. Each of the spring is cut into two pieces. First piece of spring A is (4/5) of the total length. Second piece of spring B is (5/6) of its total length. Both springs are of equal lengh initially :
Athe ratio of force constant of first piece of spring B to the first piece of spring A is (12/5)Bthe ratio of force constant of first piece of spring B to the first piece of spring A is 2Cthe ratio of force constant of second piece of spring A to the first piece of spring B is 5/3Dthe ratio of force constant of second piece of spring A to the first piece of spring B is 7/5.
The time period (T) of a spring mass system depends upon mass (m) & spring constant (k) & length of the spring (l)[k=Forcelength]. Find the relation among T, m , l & k using dimensional method.
View SolutionBlock of mass 2m is given v0 towards the right. If L is the natural length of spring constant k, find the maximum elongation of the spring.

View Solution
A ring of mass m is attached to a horizontal spring of spring constant k and natural length l0. The other end of the spring is fixed and the ring can slide on a horizontal rod as shown. Now the ring is shifted to position B and released Find the speed of the ring when the spring attains its natural length.
View SolutionWhich spring has greater value of spring constant a hard spring or a delicate spring?
View SolutionA spring of certain length and having spring constant k is cut into two pieces of length in a ratio 1:2. The spring constants of the two pieces are in a ratio :
View Solution
