The maximum energies of photoelectrons emitted by a metal are E1andE2 when the incident radiation has frequencies f1andf2 respectively. Show that Planck's constant h and the work function W0 of the metal are
h=E1−E2f1−f2,W0=E1f2−E2f1f1−f2Solution in Bengali
According to Einstein's photoelectric equation we have, E1=hf1−W0…(1)
E2=hf2−W0…(2)
E1−E2=h(f1−f2)
∴h=E1−E2f1−f2 [for E1>E2] ….(3)
Again multiplying equation (1) by f2 and equation (2) by f1 we obtain,
E1f2=hf1f2−f2W0...(4)
and E2f1=hf1f2−f1W0....(5)
Subtracting equation (5) from equation (4), we get
E1f2−E2f1=f1W0−f2W0=W0(f1−f2)
∴W0=E1f2−E2f1f1−f2
Topper's Solved these Questions
- QUANTUM THEORYBook:CHHAYA PUBLICATIONChapter:QUANTUM THEORYExercise:Section Related Question
Explore 18 Videos
- QUANTUM THEORYBook:CHHAYA PUBLICATIONChapter:QUANTUM THEORYExercise:Higher Order Thinking Skill (HOTS) Questions
Explore 26 Videos
- OPTICAL INSTRUMENTSBook:CHHAYA PUBLICATIONChapter:OPTICAL INSTRUMENTSExercise:CBSE SCANNER
Explore 8 Videos
- QUESTION PAPER OF NEET 2017Book:CHHAYA PUBLICATIONChapter:QUESTION PAPER OF NEET 2017Exercise:QUESTION PAPERS OF (NEET) (2017)
Explore 39 Videos
Similar Questions
What is photoelectric effect
View SolutionPhotoelectric current still continues when the anode is even at a slight negative potential with respect to the photo cathode. Explain.
View SolutionDefine the magnifying power of a compound microscope when the final image is formed at infinity . Why must both the objective and the eyepiece of a compound microscope has short focal lengths ? Explain.
View SolutionA molecule of a substance has permanent dipole moment p. A mole of this substance is polarised by applying a strong electrostatic field E. The direction of the field is suddenly changed by an angle of 60∘. If N is the Avogadro's number the amount of work done by the field is
View SolutionIf F1andF2 aare two vectors of equal magniudes F such that |F1.F2|=|F1×F2|,then|F1+F2| equals to
View SolutionLet E1E2andF1F2 be the chords of S passing through the point P∘ (1, 1) and parallel to the X-axis and the Y-axis, respectively. Let G1G2 be the chord of S passing through P∘ and having slope -1. Let the tangents to S at E1andE2 met at F3, and the tangents to S at G1andG2 meet at G3. Then , the points E3,F3andG3 lie on the curve
Let S be the circle in the XY-plane defined by the equation
x2+y2=4
View SolutionFor the following table, the values of f1, f0 and f2 are respectively______.
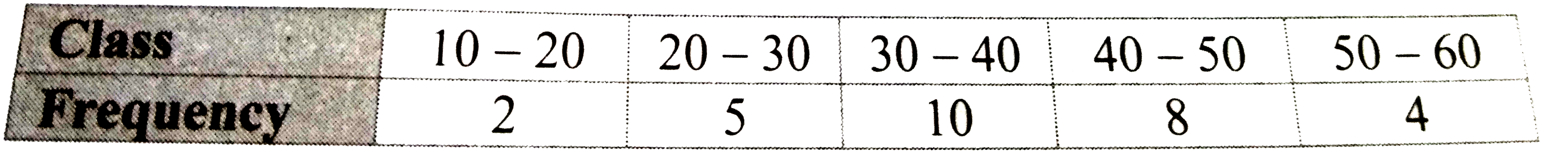
View SolutionGiven F1=1,F2=3andFn=Fn−1+Fn−2 then F5 is
View SolutionGiven F1=1,F2=3andFn=Fn−1+Fn−2 then F3 is ____.
View Solutionl+(f1−f02f1−f0−f2)×hसूत्र है:
View Solutionबहुलक =l+(f1−f02f1−f0−f2)×h में h होता है ।
View Solutionमाना कि S एक वृत्त है जो xy समतल में समीकरण x2+y2=4 के द्वारा परिभाषित है।
माना कि E1E2 और F1F2 वृत्त S की ऐसी जीवाएं हैं जो बिन्दु P0(1,1) से गुजरती हैं और क्रमश: x-अक्ष व y-अक्ष के समान्तर हैं। माना कि G1G2,S की वह जीवा है जो P0 से गुजरती है और जिसकी प्रवणता -1 है। माना कि E1 और E2 पर S की स्पर्शियां E3 पर मिलती हैं, F1 और F2 पर S की स्पर्शियां F3 पर मिलती हैं, तथा G1 और G2 पर S की स्पर्शियां G3 पर मिलती हैं। तब बिन्दु E3,F3 और G3 से गुजरने वाले वक्र का समीकरण है
View Solutionf1(x)=x+a,f2(x)=x2+bx+c and Δ=∣∣ ∣ ∣∣111f1(x1)f1(x2)f1(x3)f2(x1)f2(x2)f2(x3)∣∣ ∣ ∣∣, then Δ is independent of
View Solutionदो सदिशों F1 व F2 का परिमाण समान है जिसका मान F है। यदि |F1⋅F2|=|F1×F2| तब |F1+F2| बराबर है
View Solutionमाना कि S एक वृत्त है जो xy समतल में समीकरण x2+y2=4 के द्वारा परिभाषित है।
माना कि P वृत्त S पर स्थित एक ऐसा बिन्दु है जिसके दोनों निर्देशांक धनात्मक है। माना कि वृत्त S के बिन्दु P पर स्पर्शी निर्देशांक अक्षों को बिन्दुओं M और N पर प्रतिच्छेद करती है। तब रेखाखण्ड MN के मध्य बिन्दु से गुजरने वाले वक्र का समीकरण है
View Solution

