Two circular loops of radii 0.05 m and 0.09m are placed such that their axes coincide and their centres are 0.12m apart. Charge of 10−6C is spread uniformly on each loop. Find the potential difference between the centres of loops.Solution in Bengali
Distance between the two centres, x=0.12m
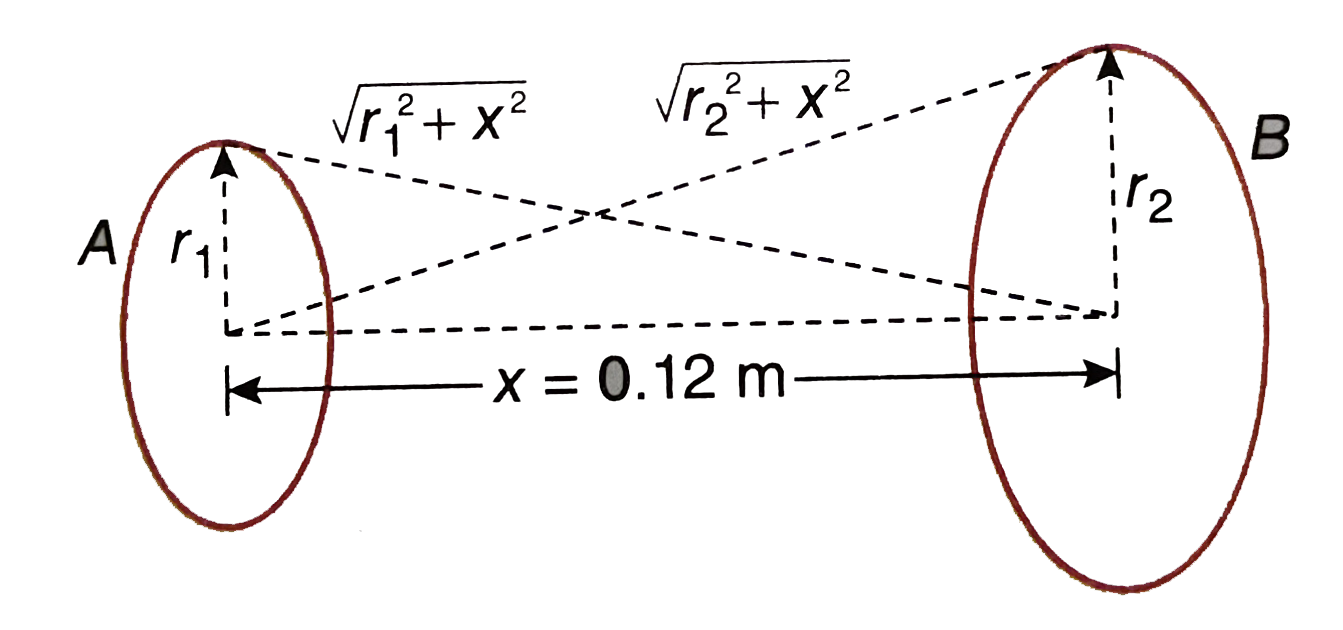
Potential at the centre of the loop A due to charge on it,
VA=14πε0q1r1=9×109×10−60.05=1.8×105V
Potential at the centre of the loop A due to charge on loop B,
V′A=14πε0q1√r22+x2=9×109×10−6√(0.09)2+(0.12)2
=9×10315×10−2=0.6×105V
Therefore total potential at the centre of loop A,
(VA)T=VA+V′A=(1.8+0.6)×105V=2.4×105V
Now potential at the centre at the centre of the loop B due to charge on it,
VB=VA=14πε0q2r2=9×109×10−60.09=1×105V
Potential at the centre of the loop B due to charge on loop A,
V′B=14πε0q2√r22+x2=9×109×10−6√(0.05)2+(0.12)2
=9×10313×10−2=0.69×105V
Therefore total potential at the centre of loop B,
(VA)T=(VB+V′B)=(1×105+0.69×105)
=1.69×105V
Thus potential difference,
(VA)T−(VB)T=(2.4−1.69)×105V
=7.1×104V≈72kV.
Topper's Solved these Questions
- ELECTRIC POTENTIAL BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC POTENTIAL EXERCISE - Section related questions
25 Videos
- ELECTRIC POTENTIAL BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC POTENTIAL EXERCISE - Higher order thinking skill (HOTS) questions
23 Videos
- ELECTRIC FIELDBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC FIELDEXERCISE - CBSE SCANNER
31 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - CBSE SCANNER
28 Videos
Similar Questions
What do you mean by potential of a charged body?
View SolutionIf the intensity at a point in an electric field is zero, will the electric potential be also zero at that point? If the electric potential be zero at a point, will the intensity be also zero at the point?
View SolutionA charge q is placed at the centre of a cube of side l. What is the electric flux passing through each face of the cube?
View SolutionA bar magnet is moved in the direction indicated by the arrow between two coils PQ and CD. Predict the directions of induced current in each coil.

View SolutionA circular loop of radius a, carrying a current I, is placed in a tow dimensional magnetic field. The centre of the loop coincides with the centre of the filed The strenght of the magnetic field at the pariphery of the loop is B. find the magnetic force on the wire.

View SolutionTwo conducting circular loops of radii R1andR2 are placed in the same plane with their centres coincidingt. Find the mutual inductane between them assuming R2<<R1.
View SolutionTwo circular loops of radii 0.05 and 0.09m, respectively, are put such that their axes coincide and their centers are 0.12m apart. A charge of 10−6C is spread uniformly on each loop. Find the potential difference between the centers of the loops.
View SolutionFind mutual inductance if we have a square loop of side r instead of a small circular loop of side r at the centre of bigger circular loop.
View SolutionRadii of two conducting circular loops are b and a respectively, where b>>a Centres of both loops coincide but planes of both loops are perpendicular each other. The value of mutual inductance for these loops
View SolutionA very long uniformly charged rod falls with a constant velocity V through the centre of a circular loop. Then the magnitude of induced emf in the loop is
View SolutionA circular loop of radius a, carrying a current I, is placed in a tow dimensional magnetic field. The centre of the loop coincides with the centre of the filed The strenght of the magnetic field at the pariphery of the loop is B. find the magnetic force on the wire.

View SolutionTwo conducting circular loops of radii R1andR2 are placed in the same plane with their centres coincidingt. Find the mutual inductane between them assuming R2<<R1.
View SolutionA circular loop of radius 0.3cm lies parallel to a much bigger circular loop of radius 20cm. The centre of the small loop is on the axis of the bigger loop. The distance between their centres is 15cm. (a) What is the flux linking the bigger loop if a current of 2.0 A flows through the smaller loop ? (b) Obtain the mutual inductance of the two loops.
View SolutionTwo con centric circular loops of radii 0.08 m and 0.10 m carry currents such that magnetic field at the centre is zero. If current in outer loop is 8 A clockwise, current in inner loop is
View SolutionTwo circular loops of radii 0.05 and 0.09m, respectively, are put such that their axes coincide and their centers are 0.12m apart. A charge of 10−6C is spread uniformly on each loop. Find the potential difference between the centers of the loops.
View Solution