The length of an iron wire is L and area of cross-section is A. The increase in length is on applying the force F on its two ends. Which of the statement is correct
Increase in length is inversely proportional to its length L
Increase in length is proportional to area of cross-section A
Increase in length is inversely proportional to A
Increase in length is proportional to Yound's modulus.
The correct Answer is:C
To solve the problem, we need to analyze the relationship between the increase in length (l) of an iron wire when a force (F) is applied, considering its original length (L), cross-sectional area (A), and Young's modulus (Y).
1. Understanding the Definitions:
- Stress (σ) is defined as the force (F) applied per unit area (A):
σ=FA
- Strain (ε) is defined as the change in length (l) per unit original length (L):
ϵ=lL
2. Applying Hooke's Law:
- According to Hooke's Law, stress is proportional to strain:
σ=Y⋅ϵ
- Substituting the definitions of stress and strain into Hooke's Law gives:
FA=Y⋅lL
3. Rearranging the Equation:
- Rearranging the equation to find the increase in length (l):
l=F⋅LA⋅Y
4. Analyzing the Relationships:
- From the equation l=F⋅LA⋅Y, we can derive the following relationships:
- The increase in length (l) is directly proportional to the applied force (F).
- The increase in length (l) is directly proportional to the original length (L).
- The increase in length (l) is inversely proportional to the cross-sectional area (A).
- The increase in length (l) is inversely proportional to Young's modulus (Y).
5. Evaluating the Statements:
- Statement 1: Increase in length is inversely proportional to its length (L) - Incorrect.
- Statement 2: Increase in length is proportional to the cross-sectional area (A) - Incorrect.
- Statement 3: Increase in length is inversely proportional to A - Correct.
- Statement 4: Increase in length is proportional to Young's modulus (Y) - Incorrect.
Conclusion:
The only correct statement is that the increase in length (l) is inversely proportional to the cross-sectional area (A).
- Stress (σ) is defined as the force (F) applied per unit area (A):
σ=FA
- Strain (ε) is defined as the change in length (l) per unit original length (L):
ϵ=lL
- According to Hooke's Law, stress is proportional to strain:
σ=Y⋅ϵ
- Substituting the definitions of stress and strain into Hooke's Law gives:
FA=Y⋅lL
- Rearranging the equation to find the increase in length (l):
l=F⋅LA⋅Y
- From the equation l=F⋅LA⋅Y, we can derive the following relationships:
- The increase in length (l) is directly proportional to the applied force (F).
- The increase in length (l) is directly proportional to the original length (L).
- The increase in length (l) is inversely proportional to the cross-sectional area (A).
- The increase in length (l) is inversely proportional to Young's modulus (Y).
- Statement 1: Increase in length is inversely proportional to its length (L) - Incorrect.
- Statement 2: Increase in length is proportional to the cross-sectional area (A) - Incorrect.
- Statement 3: Increase in length is inversely proportional to A - Correct.
- Statement 4: Increase in length is proportional to Young's modulus (Y) - Incorrect.
The only correct statement is that the increase in length (l) is inversely proportional to the cross-sectional area (A).
Topper's Solved these Questions
Similar Questions
Resistance of a conductor of length l and area of cross-section A is R. If its length is doubled and area of cross-section is halved, then find its new resistance.
View SolutionResistance of a conductor of length l and area of cross-section A is R. If its length is doubled and area of cross-section is halved, then find its new resistance.
View Solution
Knowledge Check
The length of an iron wire is L and area of cross - section is A. The increase of length l is observed on applying the force F on its two ends. Which of the following statement is correct ?
AIncrease in length is inversely proportional to LBIncrease in length is proportional to areaCIncrease in length is inversely proportional to areaDIncrease in length is proportion to Young's modulusOn suspending a weight Mg, the length l of elastic wire and area of cross section A, its length becomes double the initial length. The instantaneous stress action on the wire is
AMg/ABMg/2AC2Mg/AD4Mg/AThe mass and length of a wire are M and L respectively. The density of the material of the wire is d. On applying the force F on the wire, the increase in length is l, then the Young's modulus of the material of the wire will be
AFdlMlBFLMdlCFMldlDFdL2Ml
A wire of length 1m and area of cross section 4×10−8m2 increases in length by 0.2 cm when a force of 16 N is applied. Value of Y for the material of the wire will be
View SolutionThe resistance of wire of length l and area of cross-section a is x ohm. If the wire is stretched to double its length, its resistance would become:
View SolutionThe self-inductance L of a solenoid of area of cross-section A and length l, with N turns increase as:
View SolutionI−V characteristics of a copper wire of length L and area fo cross-section A is shown in Fig. The slope of the curve becomes
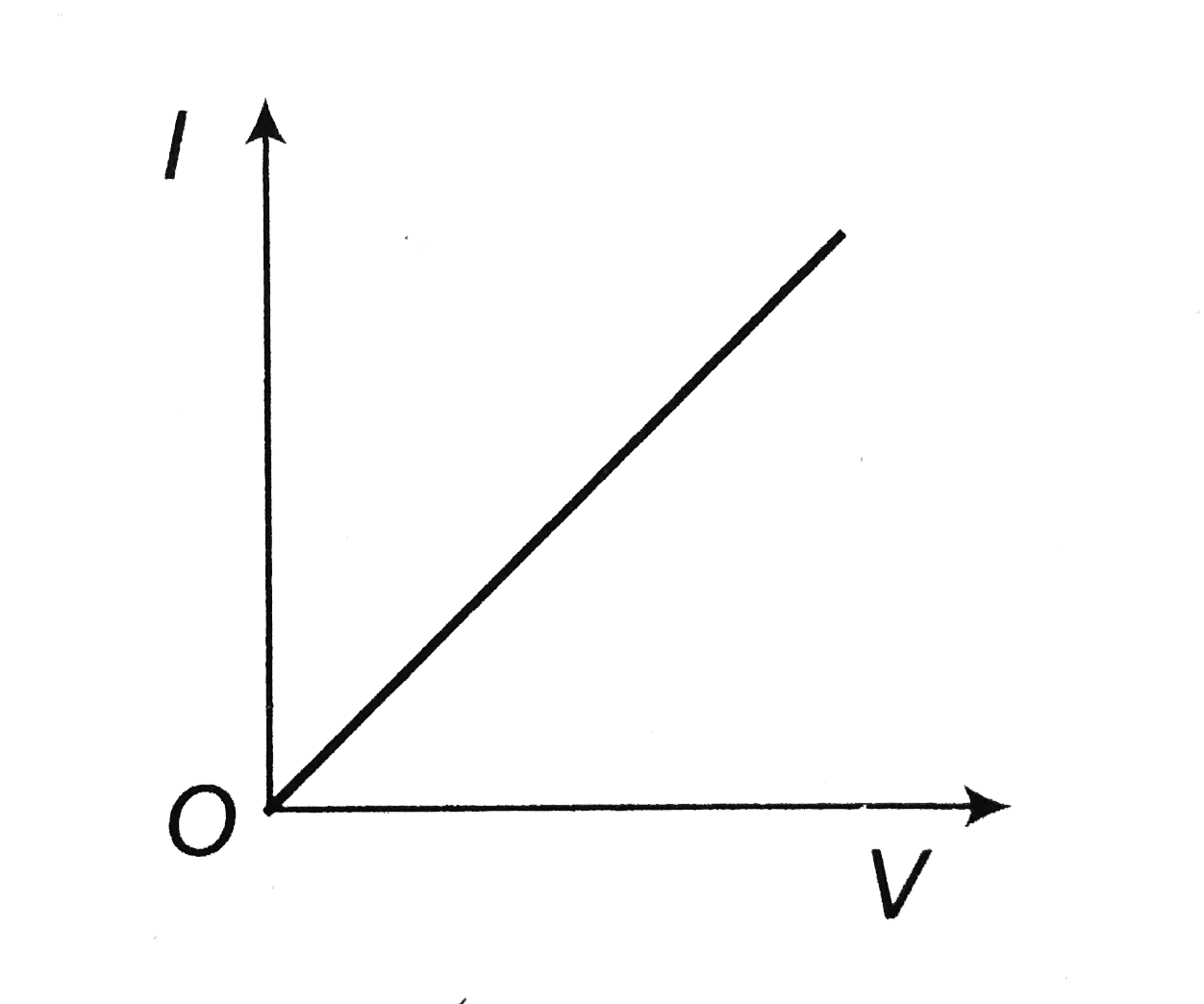
View Solutionl-V characteristic of a copper wire of length Land area of cross-section A is shown in figure. The slope of the curve becomes
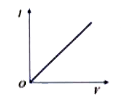
View Solution

