एक रेडियोऐक्टिव पदार्थ की अर्द्धआयु 20 मिनट है | इसके 2/3 भाग के क्षय होने में लगे समय t2 तथा 1/3 भाग के क्षय होने में लगे समय t1 में समयान्तर (t1−t2) होगा :
14 मिनट
20 मिनट
28 मिनट
7 मिनट
सूत्र N=N0(12)t/T से, 23 भाग क्षय होने पर 13=(12)t2/T तथा 13 भाग क्षय होने पर 23=(12)t1/T
∴12=(12)(t2−t(1))/T या t2−t1=T=20 मिनट |
Topper's Solved these Questions
- नाभिक Book:SHIVLAAL PUBLICATIONChapter:नाभिक Exercise:इन्जीनियरिंग एवं मेडिकल की विभिन्न प्रतियोगी प्रवेश परीक्षाओं के लिए (बोधात्मक प्रश्न)
Explore 8 Videos
- धारा विद्युत Book:SHIVLAAL PUBLICATIONChapter:धारा विद्युत Exercise:आंकिक प्रश्न
Explore 20 Videos
- परमाणु Book:SHIVLAAL PUBLICATIONChapter:परमाणु Exercise:इन्जीनियरिंग एवं मेडिकल की विभिन्न प्रतियोगी प्रवेश परीक्षाओं के लिए (वस्तुनिष्ठ प्रश्न)
Explore 72 Videos
Similar Questions
उच्च द्रव्यमान वाले नाभिकों में तीव्र नाभिकीय बलों की तुलना में कूलॉम बल का महत्त्व क्या है ?
View Solutionताम्बे (परमाणु द्रव्यमान 63.5 तथा घनत्व 8.9×103किग्रामी3) के तार का अनुप्रस्थ परिच्छेद क्षेत्रफल 10−7 मीटर2 है इसमें 1.5 ऐम्पियर धारा बहाई जाती है। यदि तार में प्रति परमाणु एक मुक्त इलेक्ट्रॉन माना जाये तो मुक्त इलेक्ट्रॉन का अनुगमन वेग ज्ञात कीजिए।
View Solutionपरमाणु की संरचना का अध्ययन सर्वप्रथम किया था :
View SolutionIf the normals at points t1andt2 meet on the parabola, then t1t2=1 (b) t2=−t1−2t1 t1t2=2 (d) none of these
View Solutionदर्शाइए कि परवलय y2=4ax पर बिंदुओं t1,t2 और t3 से बने त्रिभुज के क्षेत्रफल का परिमाण a2(t1−t2)(t2−t3)(t3−t1) है।
View Solutionतथाकथित त्रिभुजीय संख्याएँ Tn लीजिये :
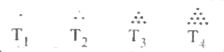
बिन्दुओ का विन्यास इस प्रकार किया गया है की इनसे एक त्रिभुज बनता है ।
यहाँ T1=1,T2=3,T3=6,T4=10 आदि आदि। क्या आप अनुमान लगा सकते है की T5 क्या है।
T6 के बारे में आप क्या कह सकते है ?
Tn के बारे में आप क्या कह सकते है ?
T8 का एक कंजेक्चर दीजिये।
View Solutionआइये हम त्रिभुजीय संख्याओं को पुनः देखे ( आकृति A 1.2 ) दो क्रमागत संख्याओं को जोड़िये। उदाहरण के लिए , T1+T2=4,T2+T3=9,T3+T4=16
T4+T5 के बारे में आपका क्या कहना है ?
Tn−1+Tn का एक कंजेक्चर बनाइये।
View SolutionThe area of triangle formed by the points points and t1,t2 and t3 on y3 =4ax is k|(t1−t2)(t2−t3)(t3−t1)| then K =
View SolutionSuppose
(x+a)n=T0+T1+T2+…+Tn
Then (T0−T2+T4−…)2+(T1−T3+T5−….)2 is equal to
View SolutionIf t_(1)+t_(2)+t_(3)=-t_(1)t_(2)t_(3) , Then points [at_(1)t_(2),a(t_(1)+t_(2))] , [at_(2)t_(3),a(t_(2)+t_(3))] And [at_(3)t_(1),a(t_(3)+t_(1))] The perpendicular of the triangle with vertices will be
View SolutionCoordinates of vertices of a triangle [a t_(3)t_(1)a(t_(3) +t_(1))], [a t_(2)t_(3), a(t_(2) + t_(3))] and [a t_(3)t_(1)a(t_(3) + t_(1))] Huh. The perpendicular of the triangle will be
View SolutionThe base of a triangle is divided into 3-equal part. If t1,t2,t3 be the tangents of the angles subtended by these parts at opposite vertex then of (1t1+1t2)(1t2+1t3)(1+1t22)=
View SolutionThe vertices of a triangle are [at1t2,a(t1+t2)],[at2,a(t2+t3)] and [at3t1,a(t3+t1)]. The co ordinates of the orthocentre of the triangle are…….
View SolutionA point moving in a straight line with uniform acceleration describes aand b feet in successive intervals of t1 and t2 seconds. Then the acceleration is 2(bt1−at2)t1t2(t1+t2)
Also if the point describes equal distances in successive times t1,t2,t3 then
1t1−1t2+1t3=3t1+t2+t3
View SolutionIn an A.P. if S_(1) = T_(1) + T_(2) + T_(3) +…+ T_(n) (n odd) S_(2) = T_(1) + T_(3) + T_(5) + …+ T_(n) , then S_(1)//S_(2) =
View SolutionIn any progression, if t2t3t1t4=t2+t3t1+t4=3(t2−t3t1−t4), then t1,t2,t3,t4 are in
View Solution

