The base of a triangle is divided into 3-equal part. If t1,t2,t3 be the tangents of the angles subtended by these parts at opposite vertex then of (1t1+1t2)(1t2+1t3)(1+1t22)=Solution in Telugu
1
2
3
4
The correct Answer is:D
Step by step video, text & image solution for The base of a triangle is divided into 3-equal part. If t_(1), t_(2), t_(3) be the tangents of the angles subtended by these parts at opposite vertex then of ((1/t_(1) + 1/t_(2))(1/t_(2) + 1/t_(3)))/((1+1/t_(2)^(2))) = by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES OF TRIANGLESBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - LECTURE SHEET EXERCISE - I (More than One correct answer Type Questions)
4 Videos
- PROPERTIES OF TRIANGLESBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - LECTURE SHEET EXERCISE - I (Matrix Matching Type Questions)
1 Videos
- PROPERTIES OF TRIANGLESBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF TRIANGLESEXERCISE - PRACTICE EXERCISE
132 Videos
- PLANESBOOK - AAKASH SERIESCHAPTER - PLANESEXERCISE - ADVANCED SUBJECTIVE TYPE QUESTIONS
30 Videos
- PROPERTIES OF VECTORSBOOK - AAKASH SERIESCHAPTER - PROPERTIES OF VECTORSEXERCISE - PRACTICE EXERCISES
55 Videos
Similar Questions
If the sines of the angle A and B of a triangle ABC satisfy the equation c2x2−c(a+b)x+ab=0 . Then the triangle
View SolutionIn a ΔABC,BC=2,CA=1+√3 and ∠C=60∘. Feet of the perpendicular from A, B and on the opposite sides BC, CA and AB are D, E and F respectively and perpendiculars are concurrerant at P.
Now match the entries of Column-I with respective entries of column-II.
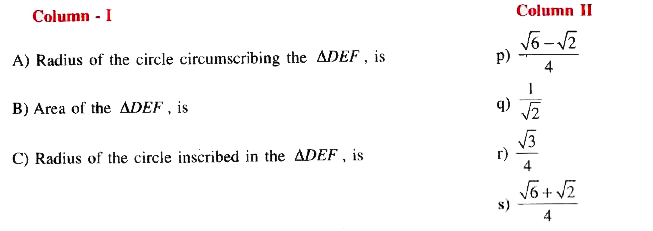
View SolutionIf a = 3, b =4 , sin A = 3/4 then ∠B=
View SolutionThe plane 2x + 3y + kz - 7 = 0 is parallel to the line whose d.r's are (2,-3,1) then k=
View SolutionIf ¯¯¯¯¯¯OA=¯i+2¯j−3¯k,¯¯¯¯¯¯OB=3¯i−2¯j+5¯kand2¯¯¯¯¯¯AC=3¯¯¯¯¯¯AB then ¯¯¯¯¯¯AC=
View SolutionThe base of a triangle is divided into three equal parts. If t1,t2,t3 are the tangents of the angles subtended by these parts at the opposite vertex, prove that (1t1+1t2)(1t2+1t3)=4(1+1t22).
View SolutionIf the normals at points t1andt2 meet on the parabola, then t1t2=1 (b) t2=−t1−2t1 t1t2=2 (d) none of these
View SolutionFind the are of triangle whose vertex are: (at_(1),(a)/(t_(1)))(at_(2),(a)/(t_(2)))(at_(3),(a)/(t_(3)))
View SolutionThe vertices of a triangle are
[at1t2,a(t1+t2)],[at2t3,a(t2+t3)], [at3t1,a(t3+t1)].
Find the orthocentre of the triangle.
View SolutionThe bae of a triangle is divided into three equal parts. If t1,t2,t3 be the tangent sof the angles subtended by these parts at the opposite vertex, prove that :
(1t1+1t2)(1t1+1t3)=4(1+1t21)
View SolutionThe coordinates of the vertices of a triangle are [at1t2,a(t1+t2)],[at2,t3,a(t2+t3)]and[at3t1,t3+t1)]. Find the coordinates of the ortocentre of the triangle.
View SolutionIf the tangents at t1andt2 to a parabola y2=4ax are perpendicular then (t1+t2)2−(t1−t2)2=
View Solutionएक त्रिभुज के शीर्षों के निर्देशांक [at2t1,a(t3+t1)],[at2t3,a(t2+t3)] व [at3t1,a(t3+t1)] हैं। त्रिभुज का लंबकेन्द्र होगा
View SolutionThe area of triangle formed by the points points and t1,t2 and t3 on y3 =4ax is k|(t1−t2)(t2−t3)(t3−t1)| then K =
View SolutionThe area of triangle formed by tangents at the parametrie points t1,t2 and t3, on y2=4ax is k|(t1−t2)(t2−t1)(t3−t1)| then K =
View Solution
