Mark correct statement(s) for →a,→b and →c shown in above diagram :

−→a−→b=→c
→a+→c=−→−b
→a+→c=→b
→b−→c=−−→−a
The correct Answer is:B, D
From triangle law :m
→a+→b=−→c
⇒ −→a−→b=→c Hence(A)
⇒ →a=→c=−→b Hence (B)
⇒ →b+→c=−→a Hence(D)
Topper's Solved these Questions
- UNIT DIMENSION, VECTOR & BASIC MATHSBook:BANSALChapter:UNIT DIMENSION, VECTOR & BASIC MATHSExercise:EXERCISE - 2 [MATRIX TYPE]
Explore 1 Video
- UNIT DIMENSION, VECTOR & BASIC MATHSBook:BANSALChapter:UNIT DIMENSION, VECTOR & BASIC MATHSExercise:EXERCISE - 3 (Miscellaneous Exercise)
Explore 20 Videos
- UNIT DIMENSION, VECTOR & BASIC MATHSBook:BANSALChapter:UNIT DIMENSION, VECTOR & BASIC MATHSExercise:EXERCISE - 1 [SINGLE CORRECT CHOICE TYPE]
Explore 34 Videos
- KINETIC THEORY OF GASESBook:BANSALChapter:KINETIC THEORY OF GASESExercise:Section-B
Explore 13 Videos
Similar Questions
Choose the correct statement
(A) If →A+→B=→A−→B then →B is a null vector
(B) If ∣∣→A+→B∣∣=∣∣→A−→B∣∣ then →A and →B are perpendicular vectors
(c) Both of the above
(D) None of the above
View SolutionGiven below in Column I are the relations between vectors a,b and c and in Column II are the orientations of a, b and c in the XY - plane . Match the relation in Column I to correct orientations in Column II.
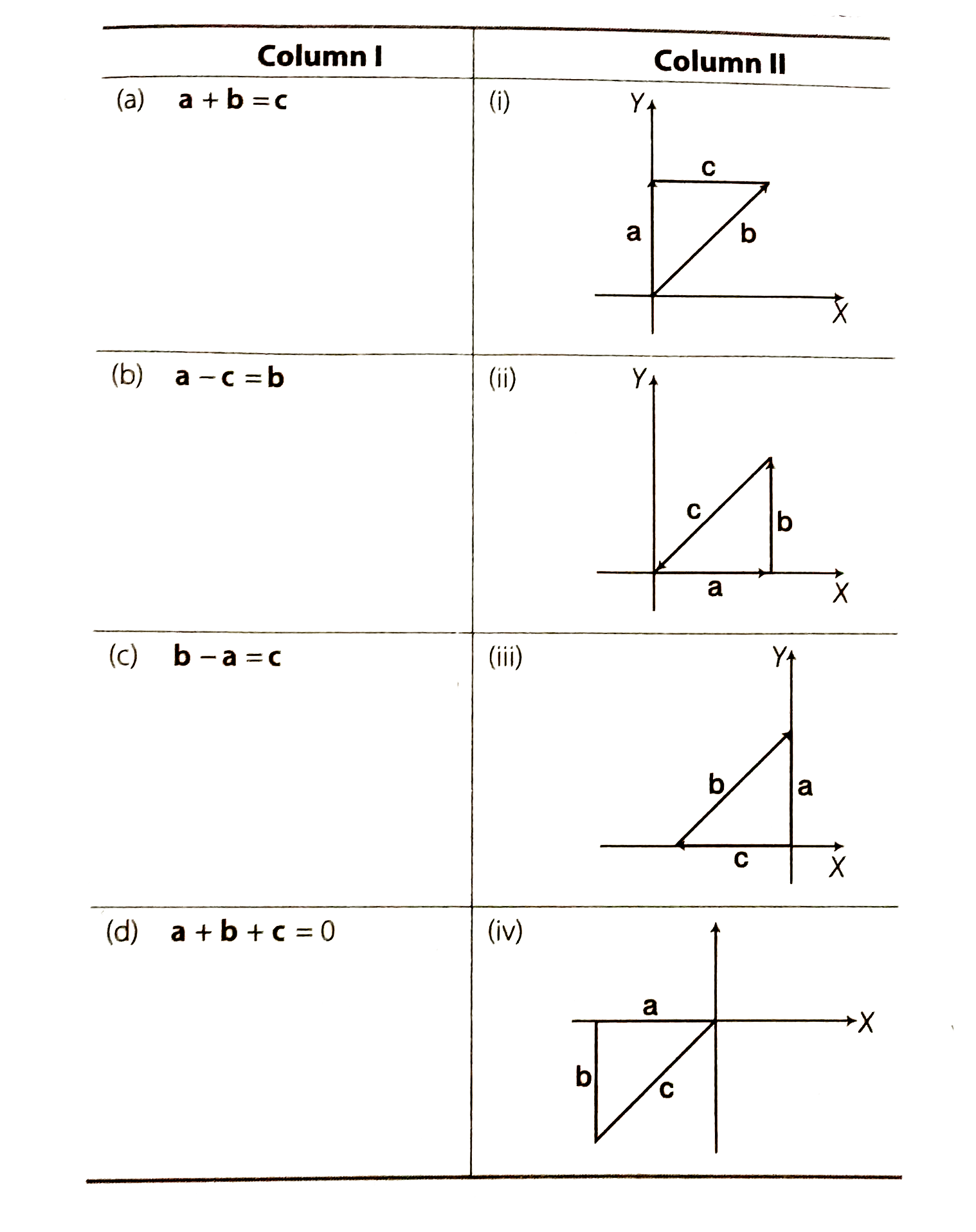
View Solution
Knowledge Check
Consider the following inequalities in respect of vector →aand→b
1. ∣∣→a+→b∣∣≤|→a|+∣∣→b∣∣
2. ∣∣→a−→b∣∣≥|→a|−∣∣→b∣∣
Which of the above is/are correct?AA) Only 1BB) Only 2CC) Both 1 and 2DD) Neither 1 nor 2Let →a.→band→c be three mutually perpendicular vectors each of unit magnitude. If →A=→a+→b+→c, →B=→a−→b+→cand→C=→a−→b−→c , then which one of the following is correct?
A1) ∣∣→A∣∣>∣∣→B∣∣>∣∣→C∣∣B2) ∣∣→A∣∣=∣∣→B∣∣≠∣∣→C∣∣C3) ∣∣→A∣∣=∣∣→B∣∣=∣∣→C∣∣D4) ∣∣→A∣∣≠∣∣→B∣∣≠∣∣→C∣∣Consider the following statements
1. For any three vectors →a,→b,→c,
→a.{(→a+→c)×(→a+→b+→c)}=0
2. For any three coplanar unit vectors
→d,→e,→f,(→d×→e).→f=1
Which of the statements given above is/are correct?A1 onlyB2 onlyCBoth 1 and 2DNeither 1 nor 2
If the vectors →a,→b and →c satisfy the condition →a+→b+→c=→0 and |→a|=3,∣∣→b∣∣=4 and |→c|=5, then show that →a.→b+→b.→c+→c.→a=−25.
View SolutionIn each of the following, fill in the blank so that the resulting statement is correct. If →a,→b,→c are three unit vectors such that →a=λ→b+μ→c an →a⋅→b=0,→a⋅→c=12 then ∣∣→b⋅→c∣∣=___________.
View SolutionIf →r.→a=→r.→b=→r.→c=12 or some nonzero vector →r, then the area of the triangle whose vertices are A(→a),B(→b)andC(→c)is(→a,→b,→c are non-coplanar) ∣∣[→a→b→c]∣∣ b. |→r| c. ∣∣[→a→b→c]→r∣∣ d. none of these
View SolutionThe vectors →a,→band→c are related by →c=→a+→b . Which diagram below illustrates this relationship ?
View SolutionIf →a+→b+→c=→0, then which of the following is/are correct?
1. →a,→b,→c are coplanar.
2. →a×→b=→b×→c=→c×→a
Select the correct answer using the code given below.
View Solution

