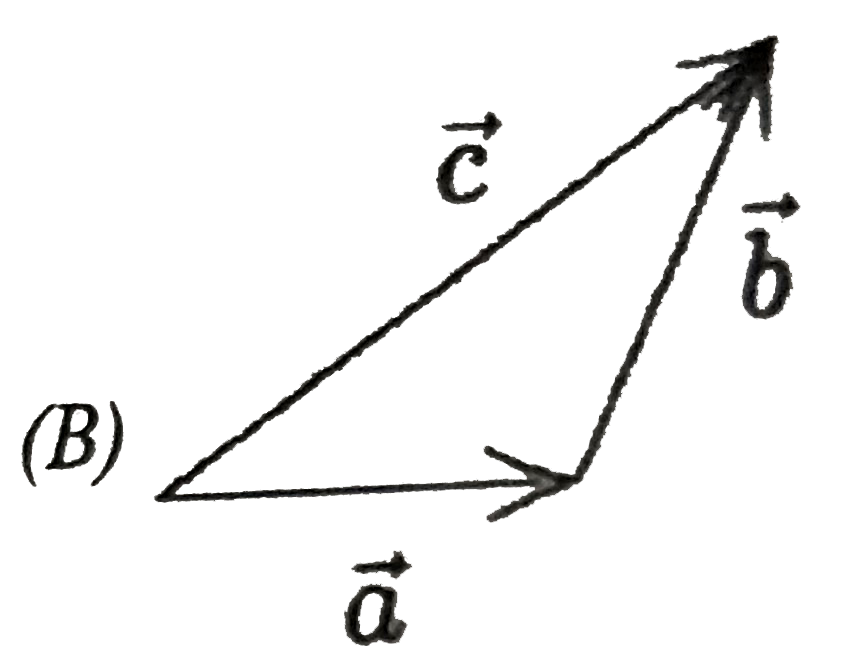
The vectors $\to a, \to b and \to c$ are related by $\to c = \to a + \to b$ . Which diagram below illustrates this relationship ?

A

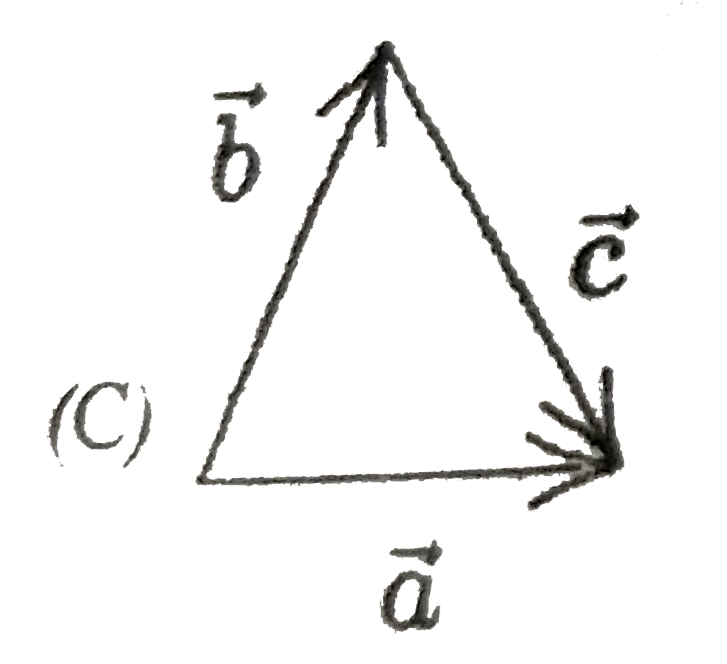
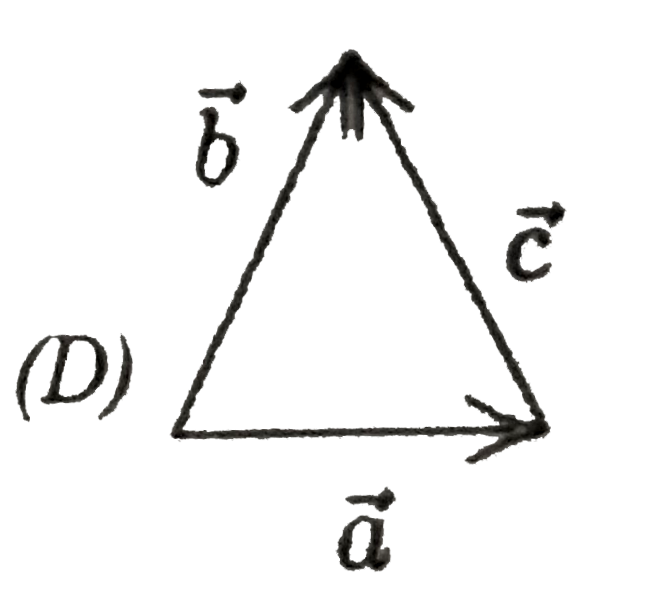
ocr_image

B

ocr_image

C

ocr_image

D

ocr_image

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:B

To solve the problem, we need to analyze the relationship given by the equation $\to c = \to a + \to b$ and determine which diagram correctly represents this vector relationship.
1. Understanding the Vector Addition:
- The equation $\to c = \to a + \to b$ indicates that vector $\to c$ is the resultant of adding vectors $\to a$ and $\to b$ .
- In vector addition, the tail of the second vector (in this case, $\to b$ ) should start from the head of the first vector (here, $\to a$ ).
2. Analyzing Diagram A:
- In Diagram A, if we start from the tail of $\to a$ , it appears that $\to b$ starts from the head of $\to a$ , but the resultant $\to c$ does not start from the head of $\to b$ .
- This does not satisfy the relationship $\to c = \to a + \to b$ .
- Conclusion: Diagram A is incorrect.
3. Analyzing Diagram B:
- In Diagram B, starting from the tail of $\to a$ , we see that $\to b$ starts from the head of $\to a$ .
- The head of $\to b$ then represents the head of $\to c$ .
- This correctly illustrates that $\to c$ is the resultant of $\to a$ and $\to b$ .
- Conclusion: Diagram B is correct.
4. Analyzing Diagram C:
- In Diagram C, if we start from the tail of $\to b$ and then move to $\to c$ , we find that this configuration implies $\to a$ is not correctly represented as the sum of $\to b$ and $\to c$ .
- This does not satisfy the relationship $\to c = \to a + \to b$ .
- Conclusion: Diagram C is incorrect.
5. Analyzing Diagram D:
- In Diagram D, similar to Diagram C, the arrangement does not show $\to c$ as the resultant of $\to a$ and $\to b$ .
- This also does not satisfy the relationship $\to c = \to a + \to b$ .
- Conclusion: Diagram D is incorrect.
Final Answer:
The correct diagram that illustrates the relationship $\to c = \to a + \to b$ is Diagram B.

Updated on:7/8/2024

|

Class 11 PHYSICS DIMENSION AND MEASUREMENT

Topper's Solved these Questions

Similar Questions

Knowledge Check

Three vector $\to A$ , $\to B$ , $\to C$ satisfy the relation $\to A \cdot \to B = 0$ and $\to A . \to C = 0$ . The vector $\to A$ is parallel to
A $\to B$
B $\to C$
C $\to B . \to C$
D $\to B \times \to C$
The vectors $\to a, \to b, \to c and \to d$ are such that $\to a \times \to b = \to c \times \to d and \to a \times \to c = \to b \times \to d$ . Which of the following is/are correct?
1. $(\to a - \to d) \times (\to b - \to c) = \to 0$
2. $(\to a \times \to b) \times (\to c \times \to d) = \to 0$
Select the correct answer using the codes given below
AA. Only 1
BB. Only 2
CC. Both 1 and 2
DD. Neither 1 nor 2
If $\to A, \to B$ and $\to C$ are three vectors, then the wrong relation is :
A $\to A + (\to B + \to C) = (\to A + \to B) + \to C$
B $\to A . (\to B + \to C) = (\to A . \to B) + \to A . \to C$
C $\to A \times (\to B + \to C) = \to A \times \to B + \to A \times \to C$
D $(\to A \times \to B) . \to C = \to A \times \to B . \to C$

BANSAL-UNIT DIMENSION, VECTOR & BASIC MATHS-Exercise

Home
Ask Doubt
Profile