If a particle moves 5m in +x- direction. Show the displacement of the particle-
5ˆj
5ˆi
−5ˆj
5ˆk
The correct Answer is:B
To show the displacement of a particle that moves 5 meters in the positive x-direction, we can follow these steps:
Step 1: Understand the Motion
The particle moves a distance of 5 meters in the positive x-direction. In physics, displacement is a vector quantity that refers to the change in position of an object.
Step 2: Identify the Magnitude of Displacement
The magnitude of the displacement is simply the distance moved in the specified direction. Here, the particle moves 5 meters.
Magnitude of Displacement = 5 meters
Step 3: Determine the Direction of Displacement
Since the particle moves in the positive x-direction, we need to represent this direction using a unit vector. The unit vector in the positive x-direction is denoted as i cap (or i).
Step 4: Write the Displacement Vector
The displacement vector can be expressed as the product of the magnitude of displacement and the unit vector in the direction of motion. Therefore, the displacement vector D can be written as:
Displacement (D)=Magnitude×Direction
Substituting the values we have:
D=5m^i
Final Answer
Thus, the displacement of the particle is:
Displacement=5^imeters
---
The particle moves a distance of 5 meters in the positive x-direction. In physics, displacement is a vector quantity that refers to the change in position of an object.
The magnitude of the displacement is simply the distance moved in the specified direction. Here, the particle moves 5 meters.
Since the particle moves in the positive x-direction, we need to represent this direction using a unit vector. The unit vector in the positive x-direction is denoted as i cap (or i).
The displacement vector can be expressed as the product of the magnitude of displacement and the unit vector in the direction of motion. Therefore, the displacement vector D can be written as:
Thus, the displacement of the particle is:
Topper's Solved these Questions
- UNIT DIMENSION, VECTOR & BASIC MATHSBook:BANSALChapter:UNIT DIMENSION, VECTOR & BASIC MATHSExercise:PRACTICE EXERCISE
Explore 4 Videos
- UNIT DIMENSION, VECTOR & BASIC MATHSBook:BANSALChapter:UNIT DIMENSION, VECTOR & BASIC MATHSExercise:EXERCISE-1 [SINGLE CORRECT CHOICE TYPE]
Explore 20 Videos
- UNIT DIMENSION, VECTOR & BASIC MATHSBook:BANSALChapter:UNIT DIMENSION, VECTOR & BASIC MATHSExercise:Exercise
Explore 10 Videos
- KINETIC THEORY OF GASESBook:BANSALChapter:KINETIC THEORY OF GASESExercise:Section-B
Explore 13 Videos
Similar Questions
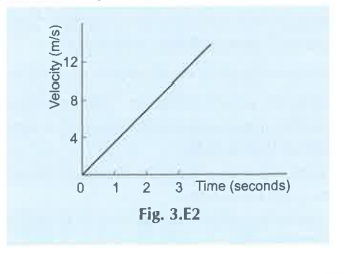
Figure 3.E2 shows the velocity -time graph for a particle moving in a fixed direction. Find the acceleration of the particle.
View SolutionThe velocity-time graph of a particle moving along a straight line is shown in the figure-given below
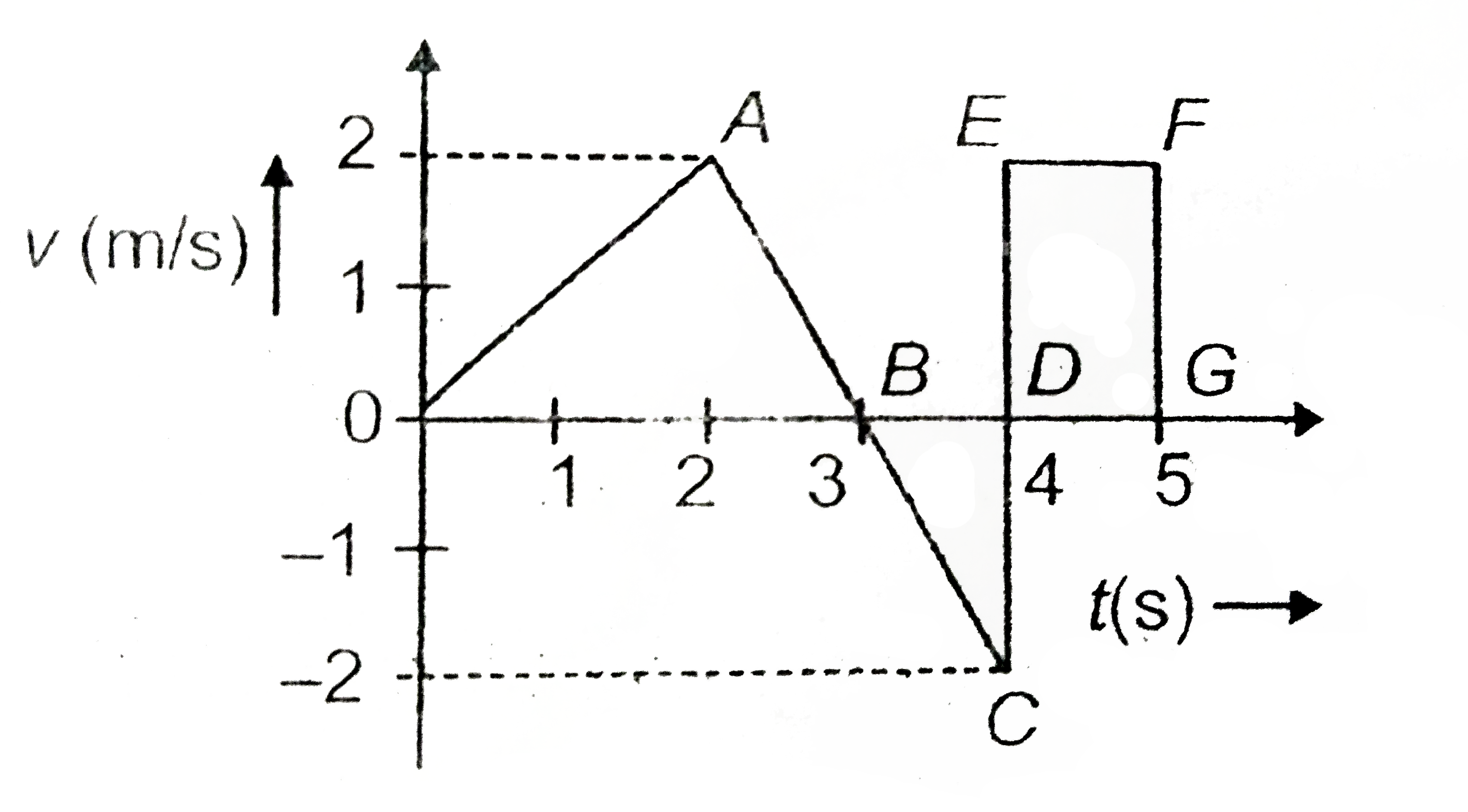
The displacement of the particle in 5 second is
View Solution
Knowledge Check
The figure shows a velocity-time graph of a particle moving along a straight line
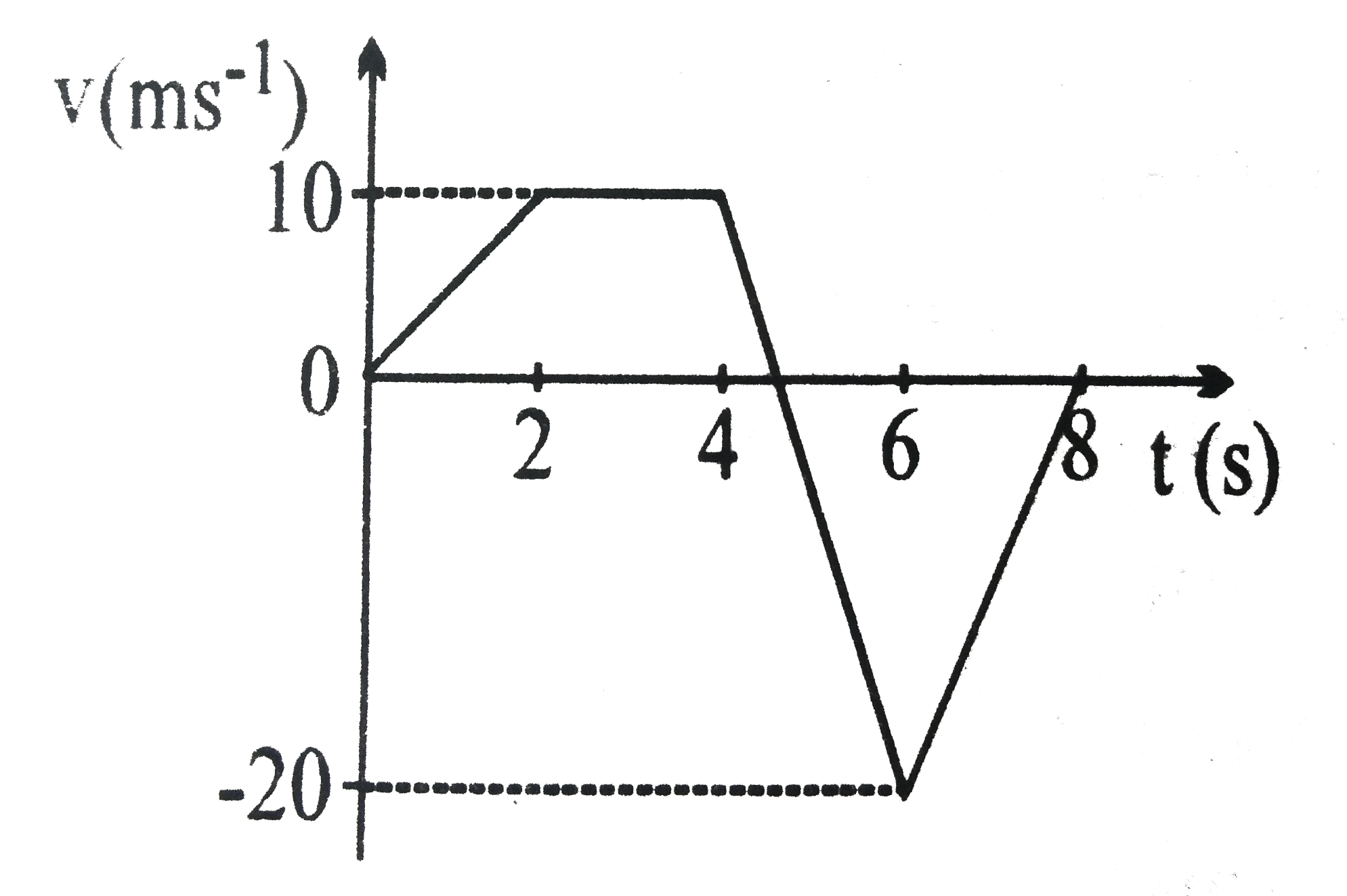
The maximum displacement of the particle isA33.3mB23.3mC18.3mDzeroThe figure shows a velocity-time graph of a particle moving along a straight line
The maximum of displacement of the particle isA33.3 mB23.3 mC18.3DzeroThe velocity - time graph of a particle moving along a straight line is shown in the figure given below
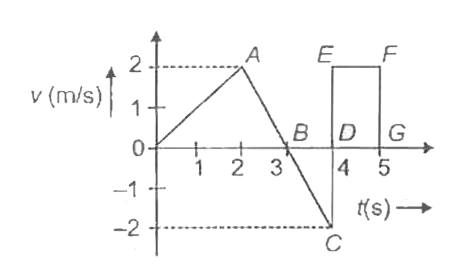
The displacement of the particle in 5 second isA0.5 mB1 mC2 mD4 m
A particle starts from the origin,goes along the "X" - axis to the point(20m,0) and then returns along the same line to the point (-20m,0 then the displacement of the particle during the trip in negative direction is....(in m )
View SolutionIn the previous problem, if the particle occupies a position x=7m at t=1s, then obtain an expression for the instantaneous displacement of the particle.
View SolutionThe diagram shows the displacement - time graph for a particle moving in a straight line. The distance (in m) coverted by the particle in the time interval t=0 to t=5s is

View SolutionThe acceleration-displacement graph of a particle moving in a straight line is as shown in figure, initial velocity of particle is zero. Find the velocity of the particle when displacement of the particle is s=12m.
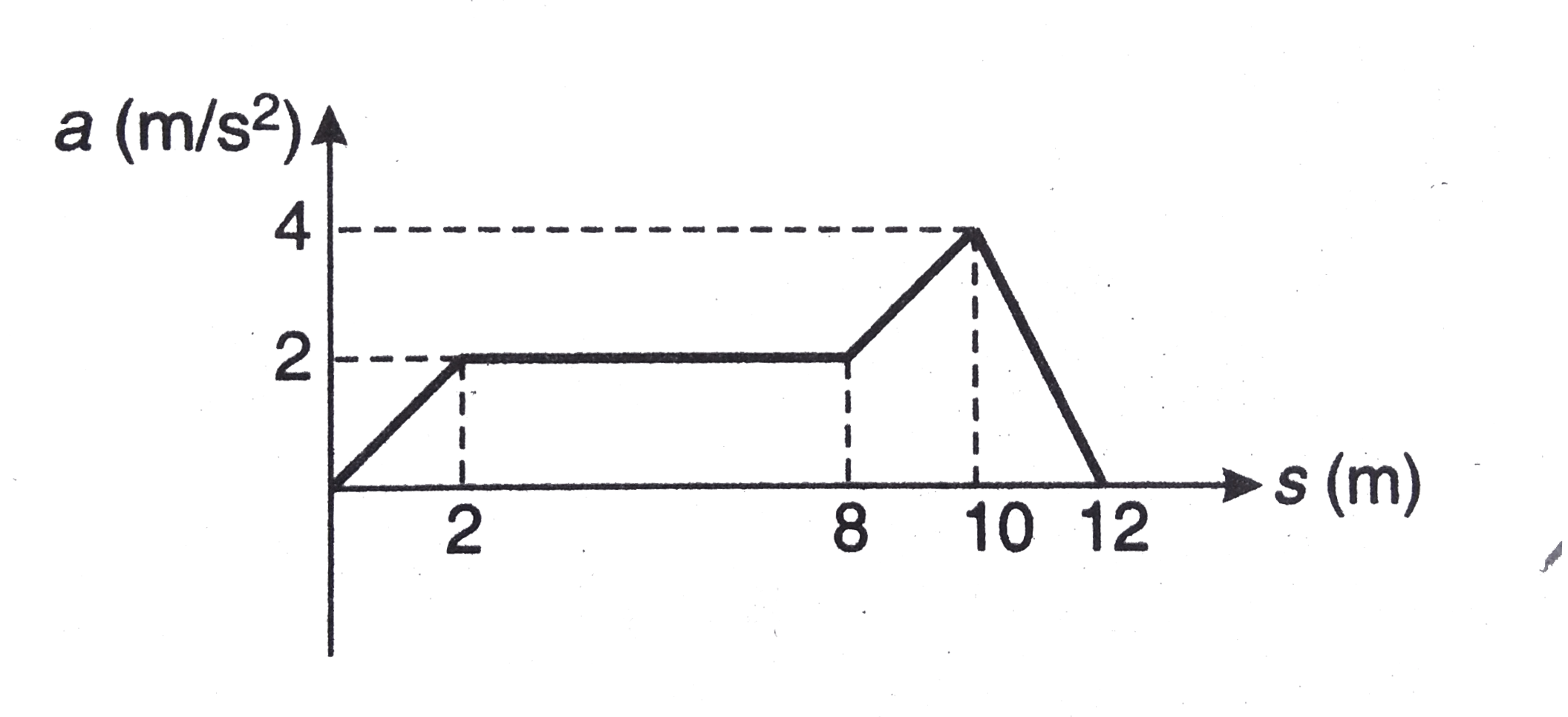
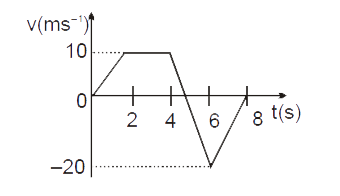
View SolutionThe figure shows a velocity-time graph of a particle moving along a straight line

Q. The maximum of displacement of the particle is
View Solution

