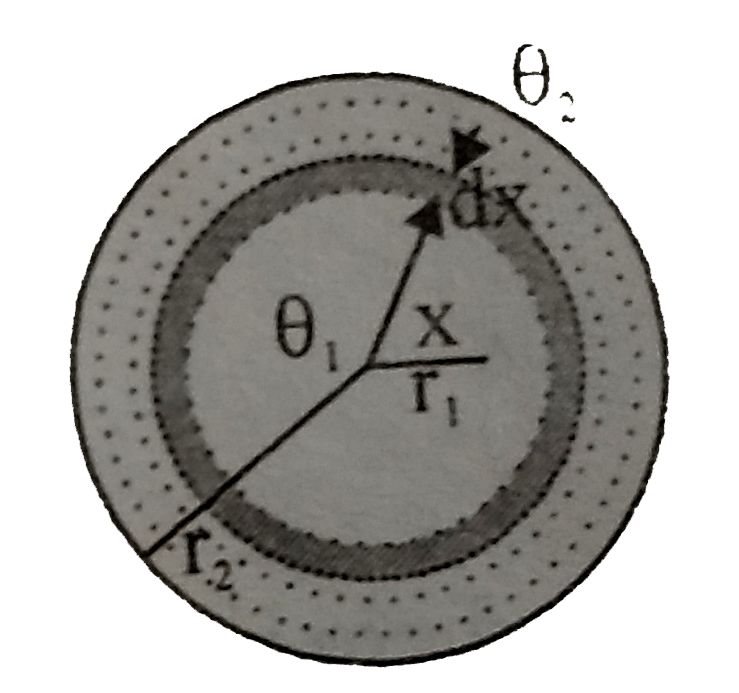
Two thin metallic spherical shells of radii r1 and r2 (r1<r2) are placed with their centres coinciding. A material of thermal conductivity K is filled in the space between the shells. The inner shells is maintained at temperature θ1 and the outer shell at temperature θ2 (θ1<θ2). Calculate the rate at which heat flows radially through the material.

Let us draw two spherical shells of radii x and x+dx concentric with the given system. Let the temperature at these shells be θ and θ+dθ respectively. The amount of heat flowing radially inward through the material between x and x+dx is
ΔQΔt=K4πx2dθdx
Thus, K4π∫θ2θ1dθ=ΔQΔt∫r2r1dxx2
K4π(θ2−θ1)=ΔQΔt(1r1−1r2)
ΔQΔt=4πKr1r2(θ2−θ1)r2−r1
Topper's Solved these Questions
Similar Questions
The space between two thin concentric metallic spherical shells of radii a and b is filled with a thermal conducting medium of conductivity k. The inner shell is maintained at temperature T1 and outer is maintained at a lower temperatureT2 . Calculate the rate of flow of heat in radially outward direction through the medium.
View SolutionTwo thin conectric shells made of copper with radius r1 and r2(r2>r1) have a material of thermal conductivity K filled between them. The inner and outer spheres are maintained at temperature TH and TC respectively by keeping a heater of power P at the centre of the two sphers. Find the value of P.
View Solution
Knowledge Check
The capacitance of two concentric spherical shells of radii R1 and R2(R2>R1) is
A4πε0R2B4πε0(R2−R1)R1R2C4πε0R1R2(R2−R1)D4πε0R1Consider two concentric spherical metal shells of radii r1 and r2(r2>r1). If the outer shell has a charge q and the inner one is grounded, then the charge on the inner shell is
A−r2r1qBzeroC−r1r2qD−qSpace between tow concentric spheres of radii r1andr2 such that r1<r2 is filled with a material of resistivity ρ. Find the resistance between inner and outer surface of the material
 Ar1r2p2Br2−r1r1r2p4πCr1r2r2−r1p4πDnone of these.
Ar1r2p2Br2−r1r1r2p4πCr1r2r2−r1p4πDnone of these.
Consider two concentric spherical metal shells of radii r1 and r2(r2>r1). Find the charge on the inner shell and charge distribution.
View SolutionA metallic spherical shell has an inner radius R1 and outer radius R2. A charge is placed at the centre of the spherical cavity. The surface charge density on the inner surface is
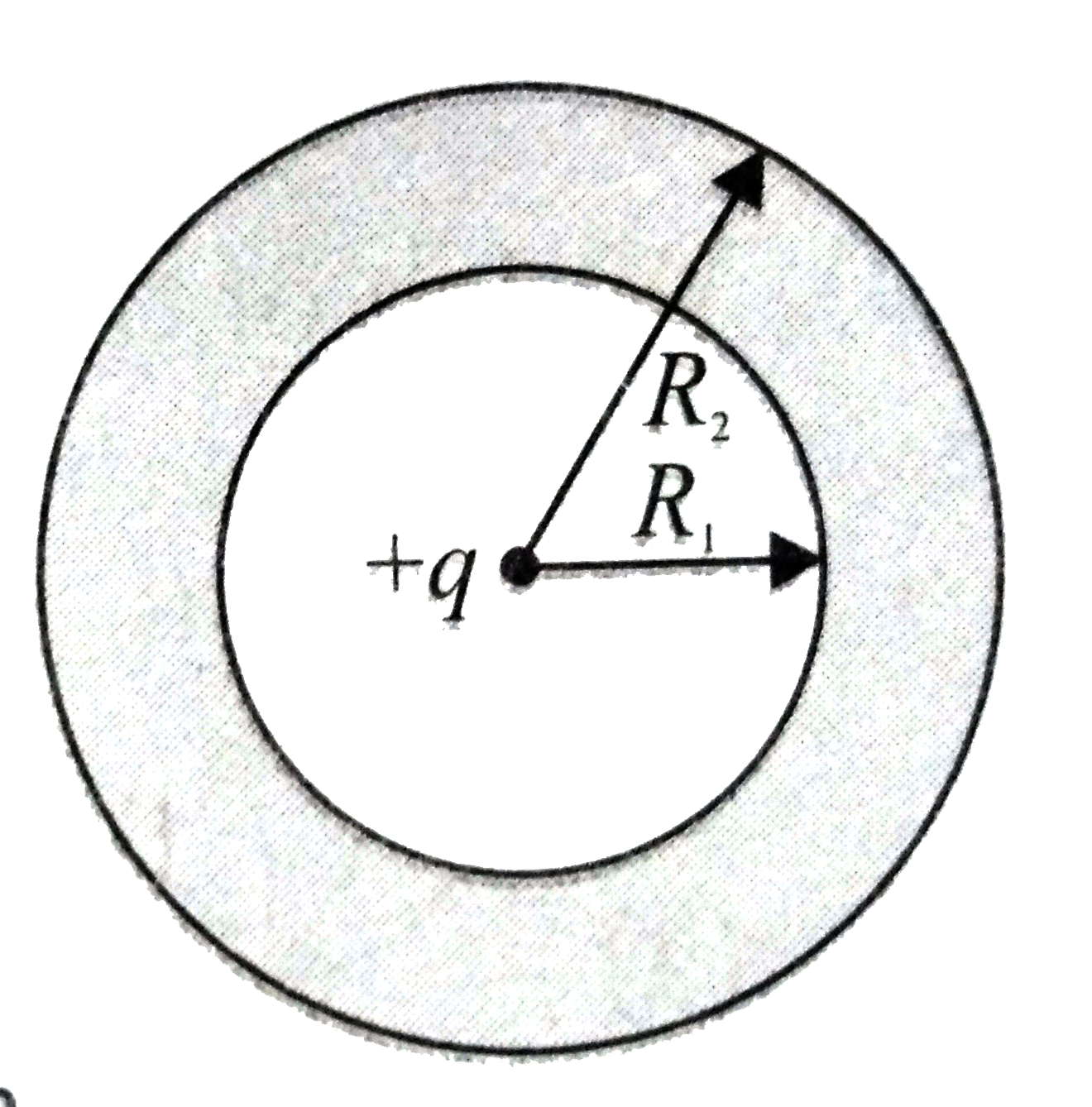
View SolutionTwo thin concentric shells made from copper with radiusr1andr2(r2>r1) have a material of thermal conductivity K filled between them. The inner and outer spheres are maintained at temperatures THandTC respectively by keeping a heater of power P at the centre of the two spheres. Find the value of P.
View SolutionA metal spherical shell has an inner radius R1 and outer radius R2. A charge Q is placed at the center of the spherical cavity. What will be surface charge density on (i) the inner surface, and (ii) the outer surface ?
View SolutionTwo identical rods are made of different materials whose thermal conductivities are K1andK2. They are placed end to end between two heat reservoirs at temperatures θ1andθ2. The temperature of the junction of the rod is

View Solution
