A spaceship is sent to investigate a planet of mass $M$ and radius $R$ . While hanging motionless in space at a distance $5 R$ from the centre of the planet, the spaceship fires an instrument package of mass $m$ , which is much smaller than the mass of the spaceship. For what angle $θ$ will the package just graze the surface of the planet?

Video Solution

Text Solution

Verified by Experts

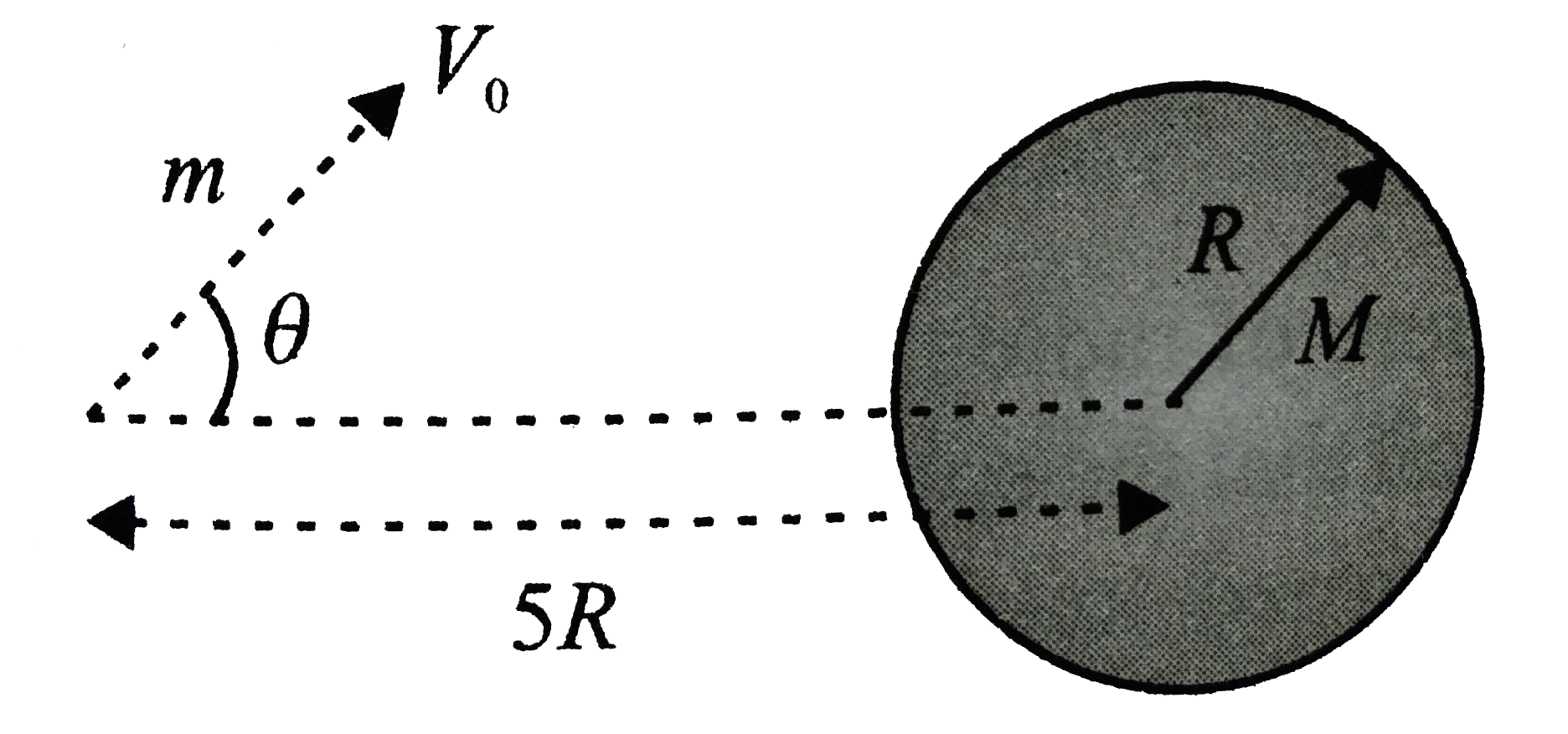
Let the speed of the instrument package is v when it grazes the surface of the planet.

Conserving angular momentum of the package about the centre of the planet $m v_{0} \times 5 R sin (π - θ) = m v R {sin 90}^{\circ}$
Conserving mechanical energy
$- \frac{G M m}{5 R} + \frac{1}{2} m v_{0}^{2} = - \frac{G M m}{R} + \frac{1}{2} m v^{2}$
$\Rightarrow \frac{1}{2} m (v^{2} - v_{0}^{2}) = \frac{4 G M m}{5 R}$
$v^{2} - v_{0}^{2} = \frac{8 G M}{5 R}$
substituting the value of v from equation (I) in equation (ii)
$25 v_{0}^{2} {sin}^{2} θ - v_{0}^{2} = \frac{8 G M}{5 R} \Rightarrow sin θ \frac{1}{5} \sqrt{1 + \frac{8 G M}{5 v_{0}^{2} R}}$
or $θ = {sin}^{- 1} ⎡ ⎢ ⎣ \frac{1}{5} \sqrt{(1 + \frac{8 G M}{5 v_{0}^{2} R})} ⎤ ⎥ ⎦$

Updated on:21/07/2023