A space vehicle approaching a planet has a speed v when it is very far from the planet At that moment tangent of its trajectory would miss the centre of the planet by distance R if the planet has mass M and radius r what is the smallest value of R in order that the resulting orbit of the space vehicle will just miss the surface of the planet?
R=rv[v2+2GMr]1/2
R=vr[1+2GMr]
R=vr[v2+2GMr]
R=2GMvr
The correct Answer is:A
Conserving angular momentum we have
mvR=mv'r…(1)[v=speedwhenspaceshipisjust→uχngthepla≠t]
conserving energy we have
12mv2=12mv2−GMmr……(2)
solving (1)&(2) we get R=rv[v2+2GMr]1/2
Topper's Solved these Questions
- MASTER PRACTICE PROBLEMBook:BANSALChapter:MASTER PRACTICE PROBLEMExercise:Comphrehension
Explore 134 Videos
- MASTER PRACTICE PROBLEMBook:BANSALChapter:MASTER PRACTICE PROBLEMExercise:Reasoning
Explore 75 Videos
- FLUID MECHANICSBook:BANSALChapter:FLUID MECHANICSExercise:PYQS AIEEE
Explore 10 Videos
- SEMICONDUCTORSBook:BANSALChapter:SEMICONDUCTORSExercise:CBSE Question
Explore 32 Videos
Similar Questions
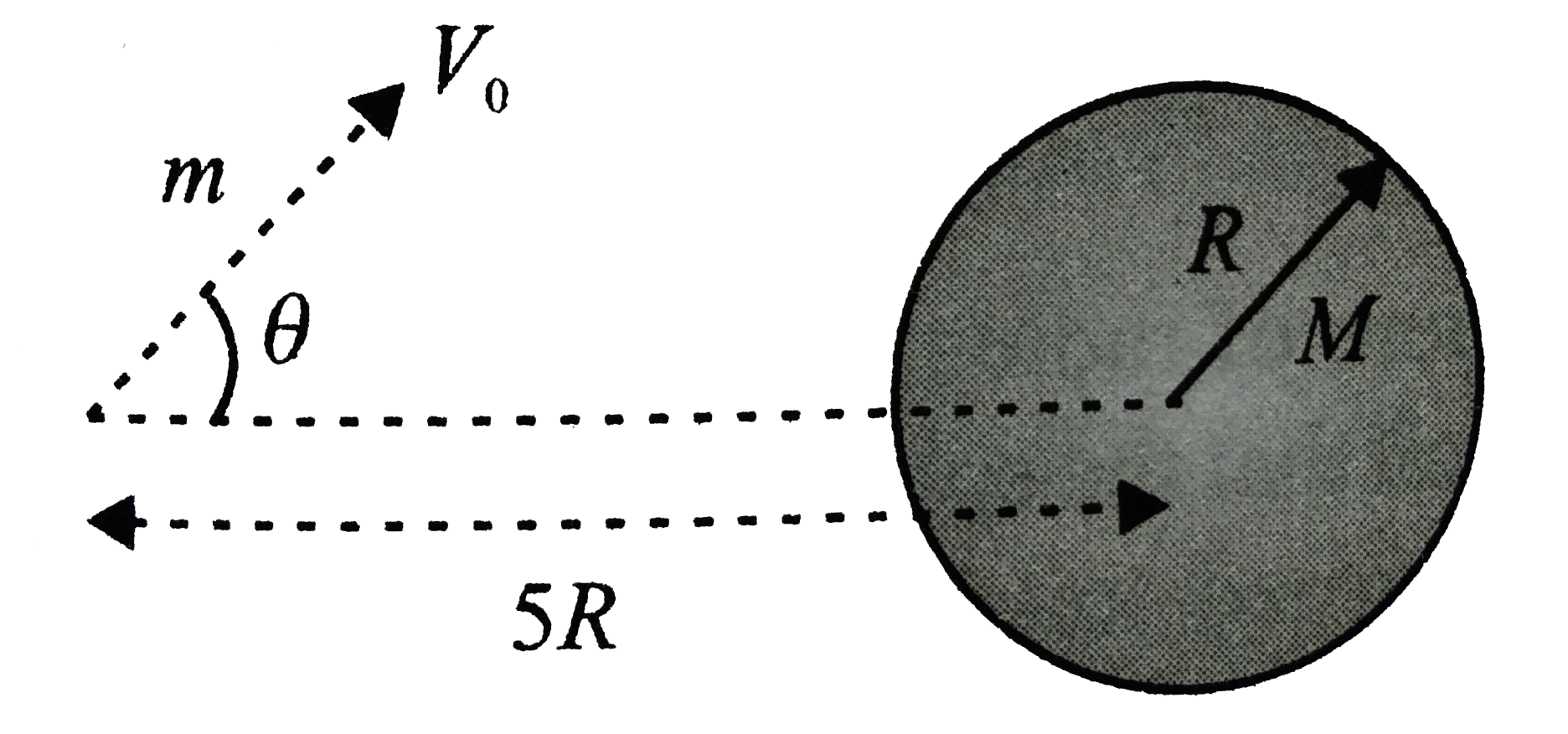
A spaceship is sent to investigate a planet of mass M and radius R. While hanging motionless in space at a distance 5R from the centre of the planet, the spaceship fires an instrument package of mass m, which is much smaller than the mass of the spaceship. For what angle θ will the package just graze the surface of the planet?
View SolutionA body is moving in a low circular orbit about a planet of mass M and radius R. The radius of the orbit can be taken to be R itself. Then the ratio of the speed of this body in the orbit to the escape velocity from the planet is :
View Solution
Knowledge Check
The angular velocity of rotation of a planet of mass M and radius R, at which the matter start to escape from its equator is
A√2GMR3B√2GMRC√2G2MRD√2GM2RA satellite can be in a geostationary orbit around earth at a distance r from the centrer. If the angular velocity of earth about its axis doubles, a satellite can now be in a geostationary orbit around if its distance from the centre is
Ar2Br2√2Cr(4)1/3Dr(2)1/3If ve is the escape velocity of a body from a planet of mass 'M' and radius 'R. Then the velocity of the satellite revolving at height 'h' from the surface of the planet will be
Ave√RR+hBve√2RR+hCve√R+hRDve√R2(R+h)
A particle at a distance r from the centre of a uniform spherical planet of mass M radius R (ltr) has a velocity of magnitude v.
View SolutionWhat is the mass of the planet that has a satellite whose time period is T and orbital radius is r?
View SolutionWhat is the minimum energy required to launch a satellite of mass m from the surface of a planet of mass M and radius R in a circular orbit at an altitude of 3R ?
View SolutionA spherical planet far out in space has mass 2M and radius a. A particle of mass m is falling freely near its surface. What will be the acceleration of that particle ?
View SolutionA body of mass m at inifnity is approaching the centre of a hypothetical hollow planet of mass M and radius R. The speed of the body when it passes the centre of the planet through a diametrical tunnel is
View Solution

