A block speed of mass m and a pan of equal mass are connected by a string going over a smooth light pulley. Initially, the system is at rest, then a particle of mass m falls on the pan ad sticks to it. If the particle strikes the pan with a speed v, find the speed with which the system moves just after the collision.
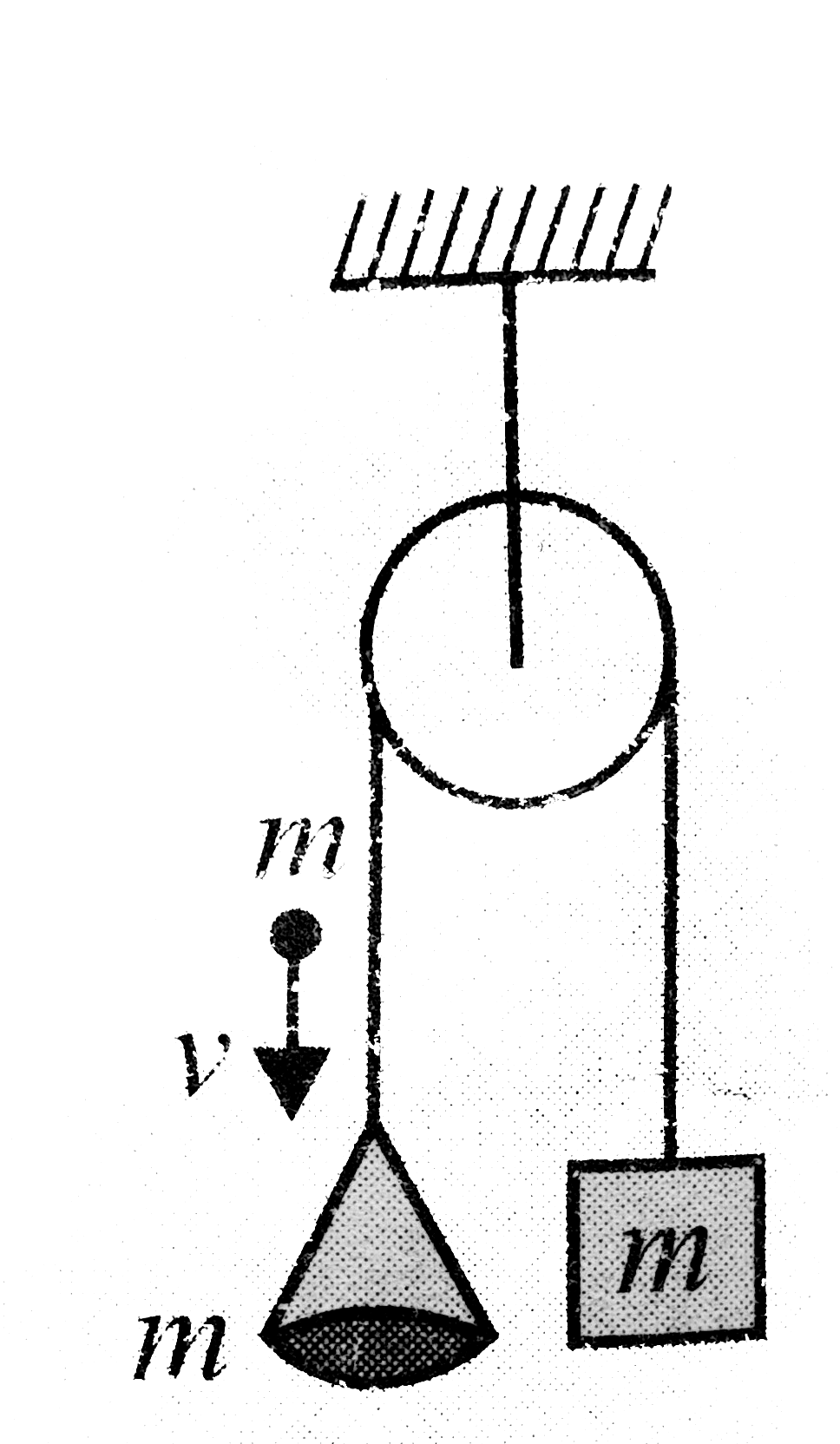
Let the required speed be V.
As there is sudden change in the speed of the block, the tension must change by a large amount during the collision.
Let N = magnitude of the contact force between the particle and the pan
T=tension in the string
Consider the impulse imparted to the particle. The force is N is in upward direction and the impulse is ∫N dt. This should be equal to the change in its momentum.
Thus, ∫N dt=mu−mV. ....(i)
Similarly considering the impulse imparted to the pan,
∫(n−T)dt=mV....(ii)
and that to the block, ∫Tdt=mV .....(iii)
Adding(ii)and(iii),
∫Ndt=2mV
comparing with (i)
mu−mV=2mV or V=u/3.
Topper's Solved these Questions
- CENTRE OF MASS & MOMENTUM CONSERVATIONBOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - Solved Examples
15 Videos
- CENTRE OF MASS & MOMENTUM CONSERVATIONBOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - Practice Exercise
20 Videos
- GRAVITATIONBOOK - BANSALCHAPTER - GRAVITATIONEXERCISE - EXERCISE -4 Section - B
6 Videos
Similar Questions
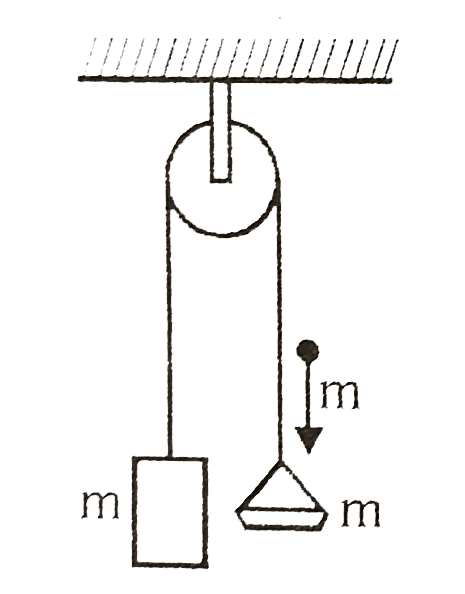
A block of mass m and α pan of equla mass are connected by a string going over a smooth light pulley as shwon in figure. Initially the systemis at rest when a particle of mass m falls on the pan and sticks to it. If the particle strikes thepan witha speed v find the speed with which the system moves just after the collision.
View SolutionA particle of mass 2m moving with velocity v strikes a stationary particle of mass 3m and sticks to it. The speed of the system will be
View Solution
Knowledge Check
Two masses m and M(>m) are joined by a light string passing over a smooth light pulley. The centre of mass of the system moves with an acceleration
 Ag(M−mM+m) downwardBg(M−mM+m)2 downwardCg(M−mM+m)2 upward if M<mDzero
Ag(M−mM+m) downwardBg(M−mM+m)2 downwardCg(M−mM+m)2 upward if M<mDzeroTwo bodies of masses m1andm2 are connected by a light string going over a smooth lilght pulley at the end of an incline. The mass1 lies on the incline m2 hangs vertically. The system is t rest. Find the angle of the incline and the fore exerted by the incline on the body of mass m_1.
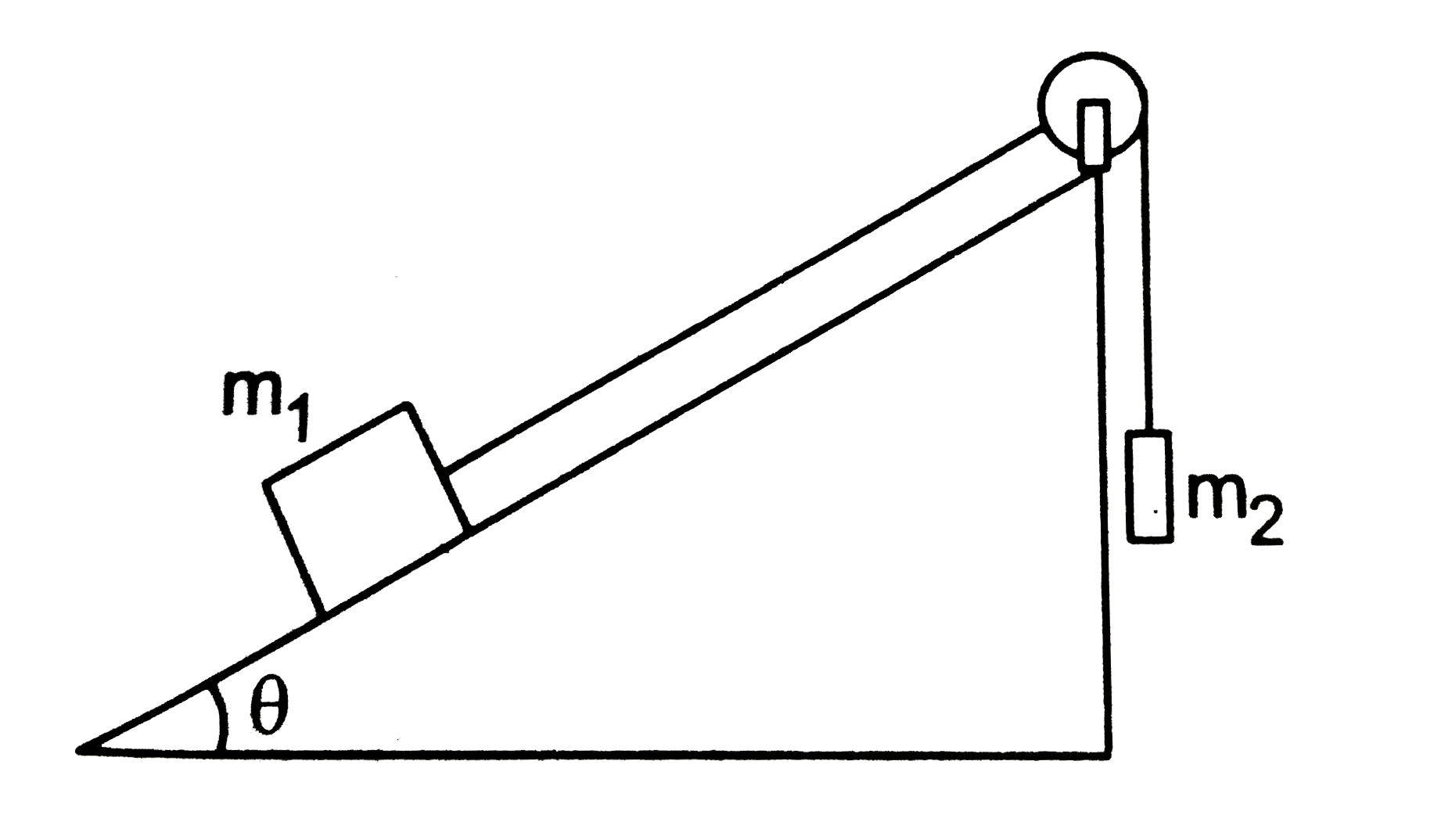 Asinθ=2m2m1 , N=m1gcosθBsinθ=m2m1 , N=m1gcosθCsinθ=m2m1 , N=m1gsinθDsinθ=m2m1 , N=4m1gcosθ
Asinθ=2m2m1 , N=m1gcosθBsinθ=m2m1 , N=m1gcosθCsinθ=m2m1 , N=m1gsinθDsinθ=m2m1 , N=4m1gcosθA particle of mass m moving with velocity v strikes a stationary particle of mass 2m and sticks to it. The speed of the system will be.
Av//2B2 vCv//3D3 v
A particle of mass 2m moving with velocity v strikes a stationary particle of mass 3m and sticks to it . The speed of the system will be
View SolutionA particle of mass m, collides with another stationary particle of mass M. If the particle m stops just after collision, then the coefficient of restitution for collision is equal to
View SolutionA pan of mass m=1.5kg and a block of mass M=3kg are connected to each other by a light inextensible string, passing over a light pulley as shown in Fig. Initially, the block is resting on a horizontal floor. A ball of mass m0=0.5kg collides with the pan at a speed v0=20m/s. Consider this instant of collision as t=0. Assume collision to be perfectly inelastic. Now, Fig. answer the following questions based on the above information.

Find the velocity of pan + ball system at t=2.6s. Assume that the block comes to rest instantaneously after striking the floor.
View SolutionA pan of mass m=1.5kg and a block of mass M=3kg are connected to each other by a light inextensible string, passing over a light pulley as shown in Fig. Initially, the block is resting on a horizontal floor. A ball of mass m0=0.5kg collides with the pan at a speed v0=20m/s. Consider this instant of collision as t=0. Assume collision to be perfectly inelastic. Now, Fig. answer the following questions based on the above information.

Find the time t at which the block strikes the floor for the first time
View SolutionA pan of mass m=1.5kg and a block of mass M=3kg are connected to each other by a light inextensible string, passing over a light pulley as shown in Fig. Initially, the block is resting on a horizontal floor. A ball of mass m0=0.5kg collides with the pan at a speed v0=20m/s. Consider this instant of collision as t=0. Assume collision to be perfectly inelastic. Now, Fig. answer the following questions based on the above information.

. Find the maximum height reached by the block alter the second jerk.
View Solution