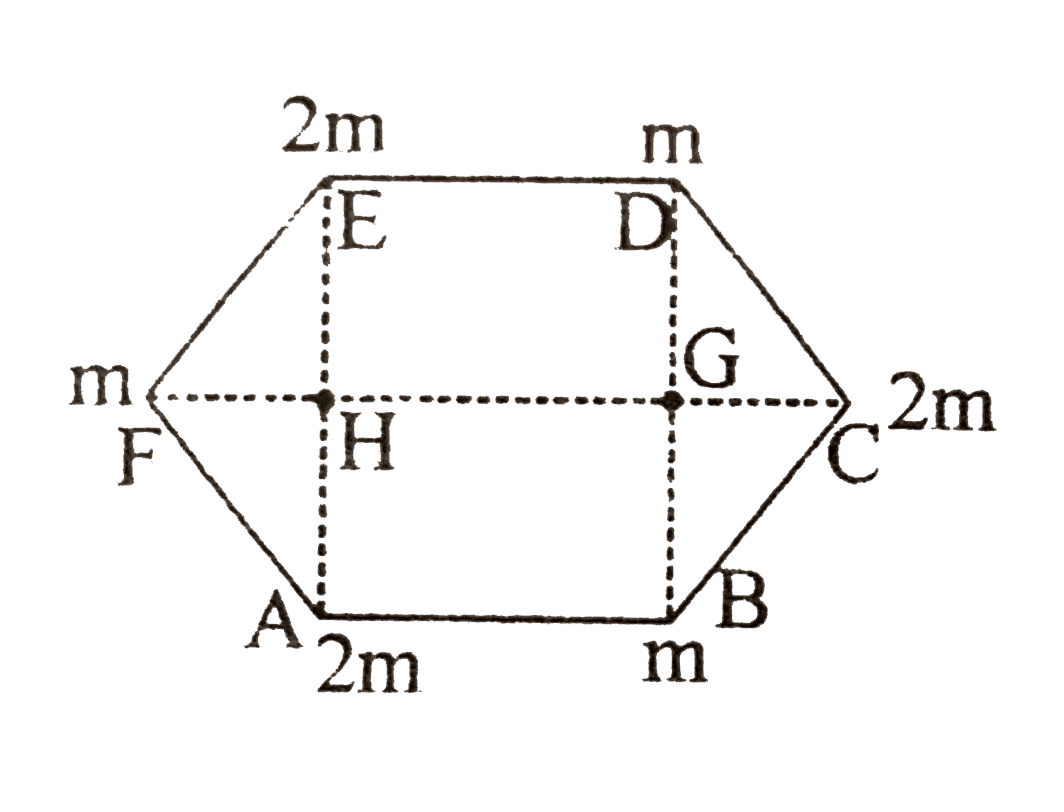
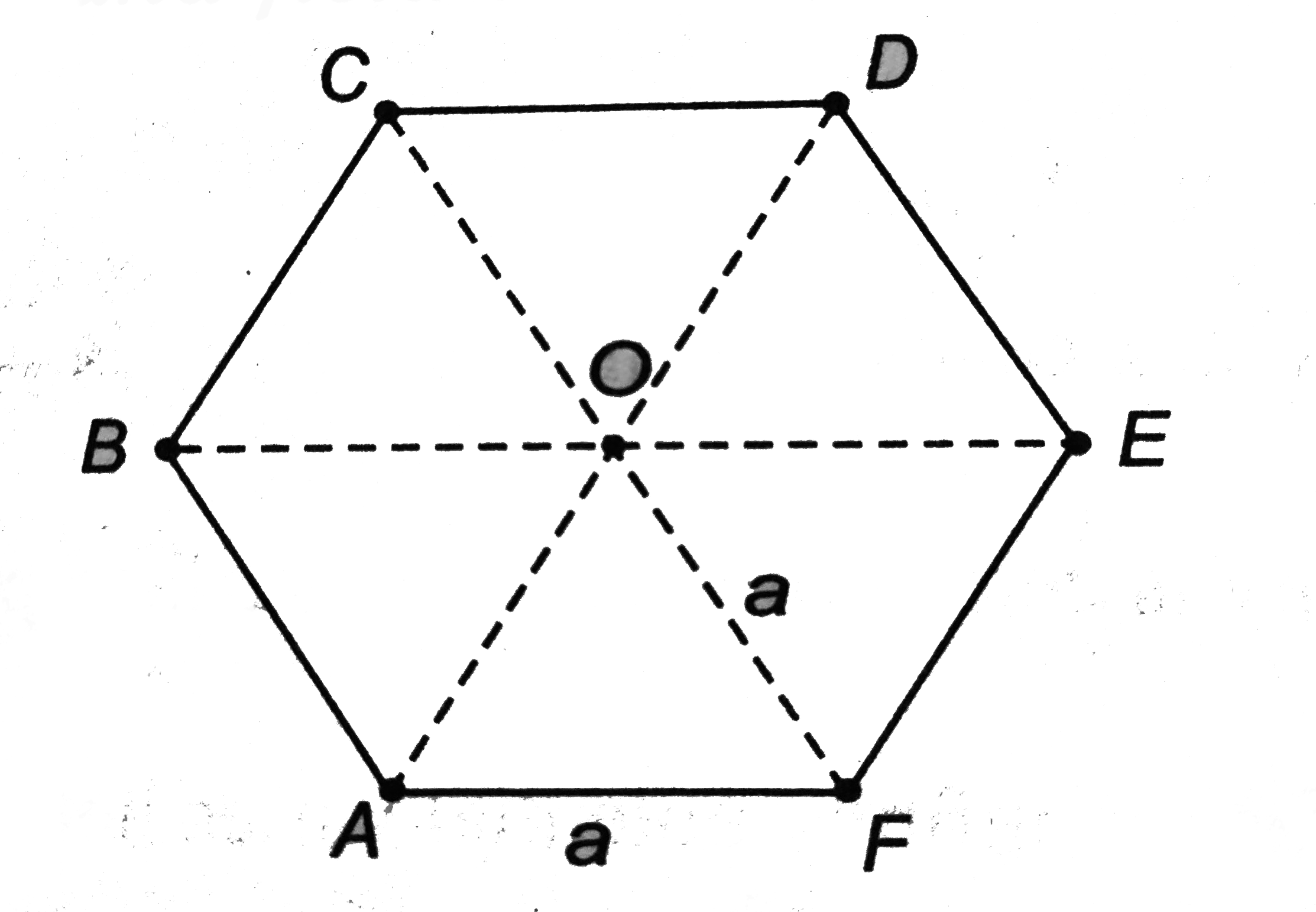
Find the position of centre of mass for a system of particles places at the vertices of a regular hexagon as shown in figure
Video Solution
Text Solution
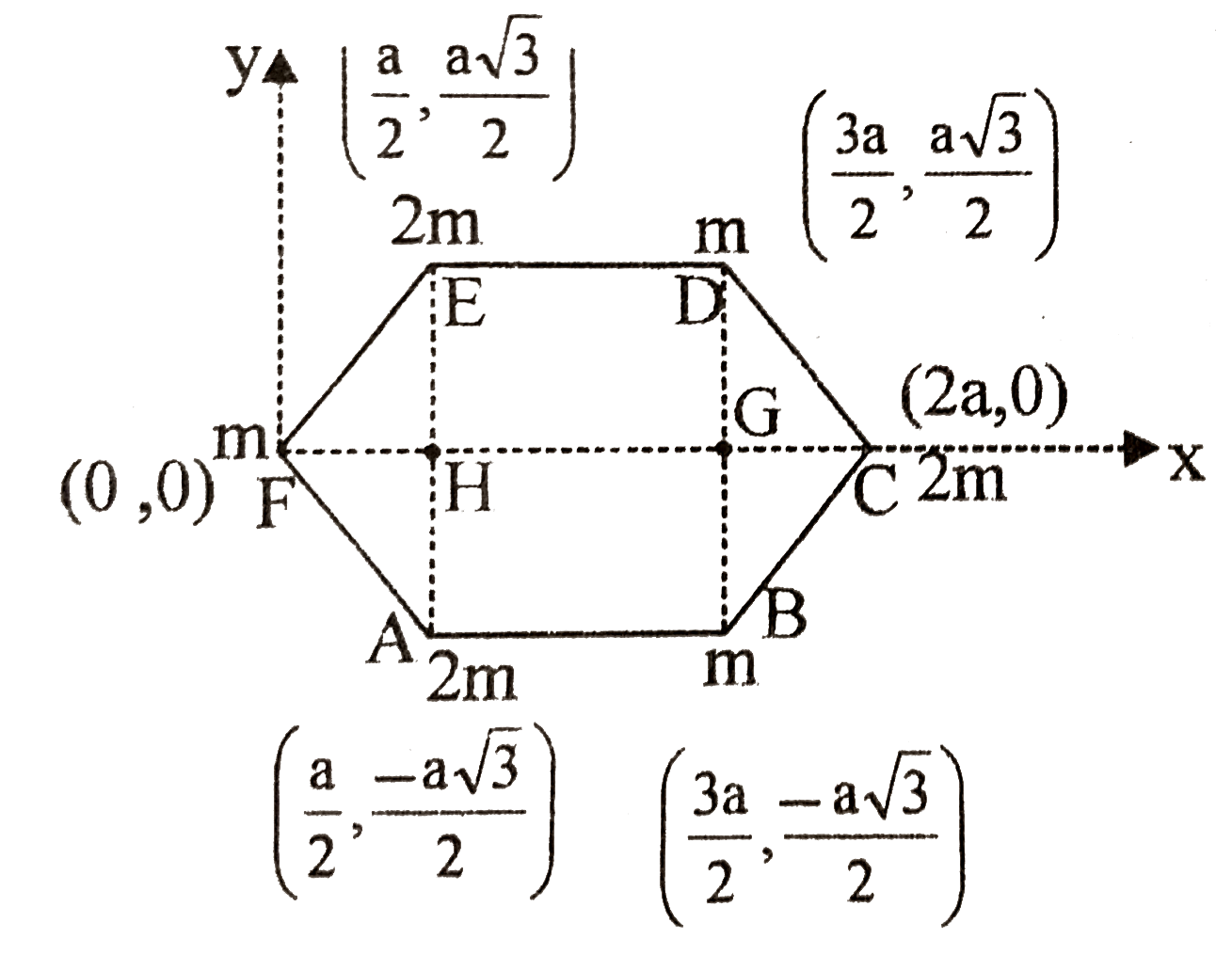
xcm=ΣmixiΣmi
=m×0+2m×a2+m×3a2+2m×2a+m×3a2+2m×a2m+2m+m+2m+m+2m
xcm=a
ycmΣmiyiΣmi
=m×0+2m×a√32+m×a√32+2m×0+m×(−a√32)+2m×(−a√32)9m
ycm=0
c.m:(a,0)
|
Topper's Solved these Questions
- CENTRE OF MASS & MOMENTUM CONSERVATIONBook:BANSALChapter:CENTRE OF MASS & MOMENTUM CONSERVATIONExercise:Solved Examples
Explore 15 Videos
- CENTRE OF MASS & MOMENTUM CONSERVATIONBook:BANSALChapter:CENTRE OF MASS & MOMENTUM CONSERVATIONExercise:Practice Exercise
Explore 20 Videos
- GRAVITATIONBook:BANSALChapter:GRAVITATIONExercise:EXERCISE -4 Section - B
Explore 6 Videos
Similar Questions
Knowledge Check
The position of centre of mass of a system of particles does not depend upon
Amasses of particlesBforces on particlesCposition of the particlesDrelative distance between the particlesThe position of center of mass of a system of particles does not depend upon the
Amasses of the particlesBforces on the particlesCpositions of the particlesDrelative distance between the particles
Find centre of mass of a system of three particle kept at the corner equilateral triangle as shown in figure
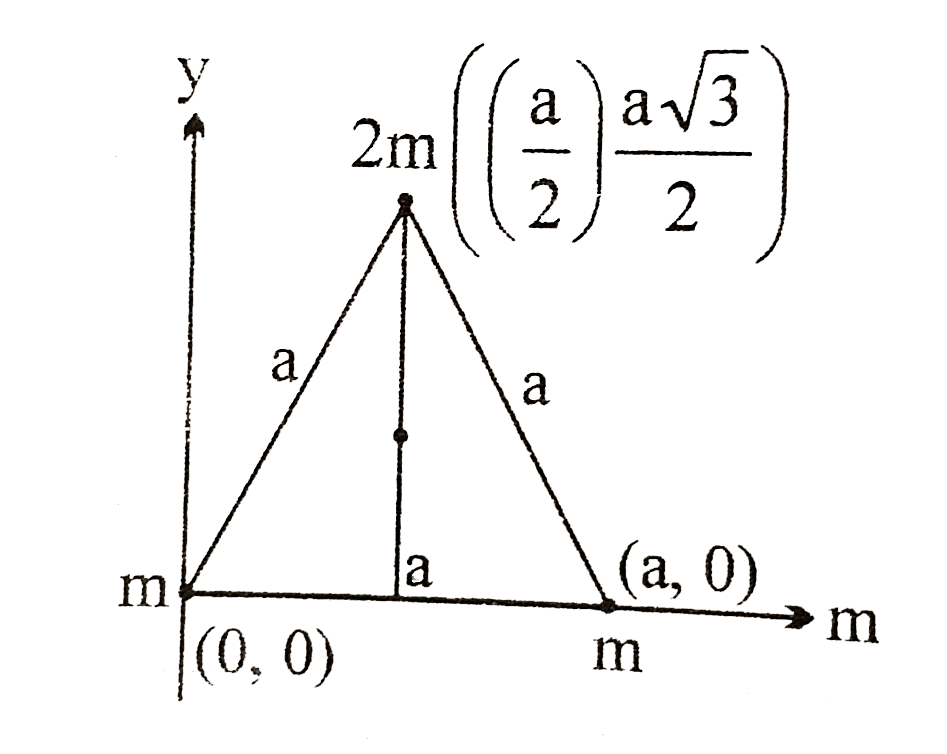
View SolutionFind out the position of centre of mass of the figure shown below.
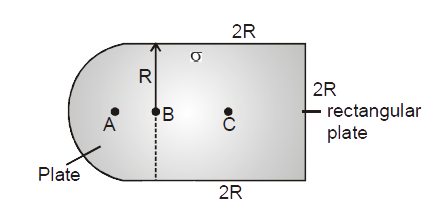
View SolutionFind the position of centre of mass of the section shown in figure

View SolutionFind the position of centre of mass of the uniform lamina shown in figure.
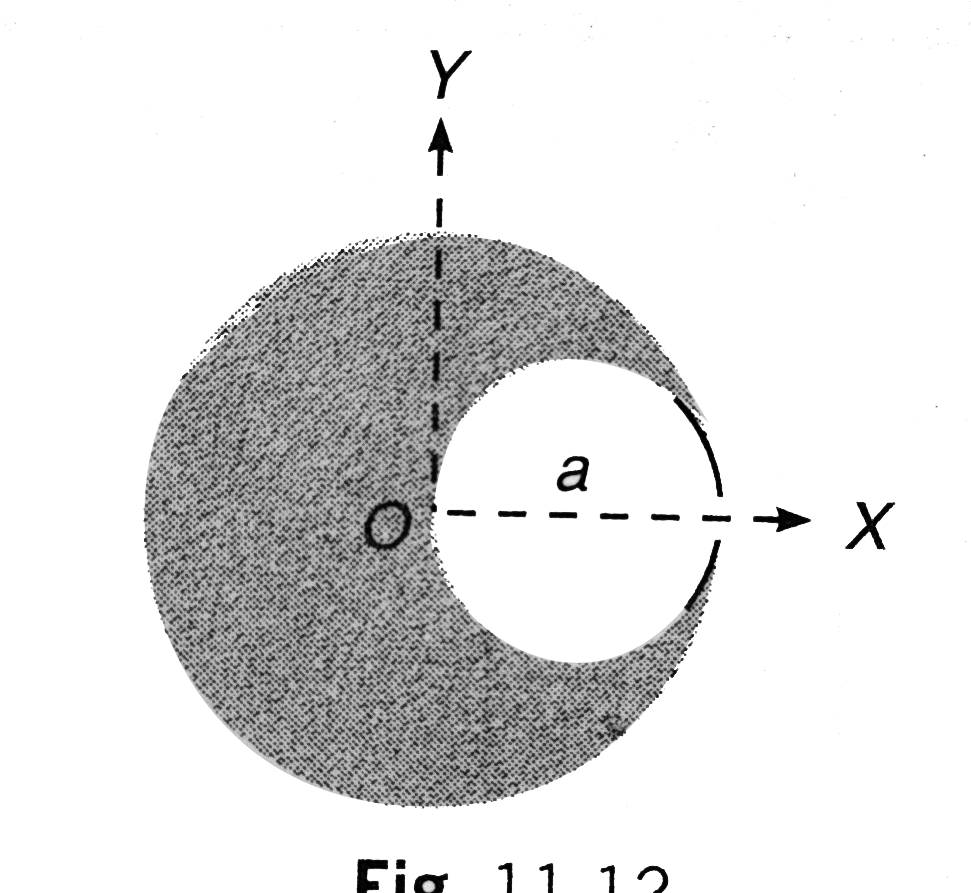
View SolutionFind the velocity of center of mass of the system shown in the figure.

View SolutionFour point masses easch of mass 'm' are placed at four vertieces A, B, C, nd D of a regular hexagon of side 'a' as shown in figure , Find gravitational potential and field strength at the centre O of the hexagon.
 .
.
View Solution