A vibrating string of certain length $l$ under a tension $T$ resonates with a mode corresponding to the first overtone (third harmonic ) of an air column of length $75 c m$ inside a tube closed at one end. The string also generates $4 b e a t s / s$ with a tuning fork of frequency $n$ . Now when the tension of the string is slightly increased the number of beats reduces to $2$ per second. Assuming the velocity of sound in air to $340 m / s$ , the frequency $n$ the tuning fork in $H_{Z}$ is
(a) $344$
(b) $336$
(c ) $117.3$
(d) $109.3$

A

$344$

B

$336$

C

$117.3$

D

$109.3$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

As string and tube are in resonance $f_{1} = f_{2}$
$| f_{1} - n | = 4 H z$ .
When $T$ increase, $f_{1}$ also increases. It is given that beat frequency decreases to $2 H z$ .
$\Rightarrow n - f_{1} = 4$
$n = 4 + f_{1}$
as $f_{1} = f_{2}$
$n = 4 + f_{2}$

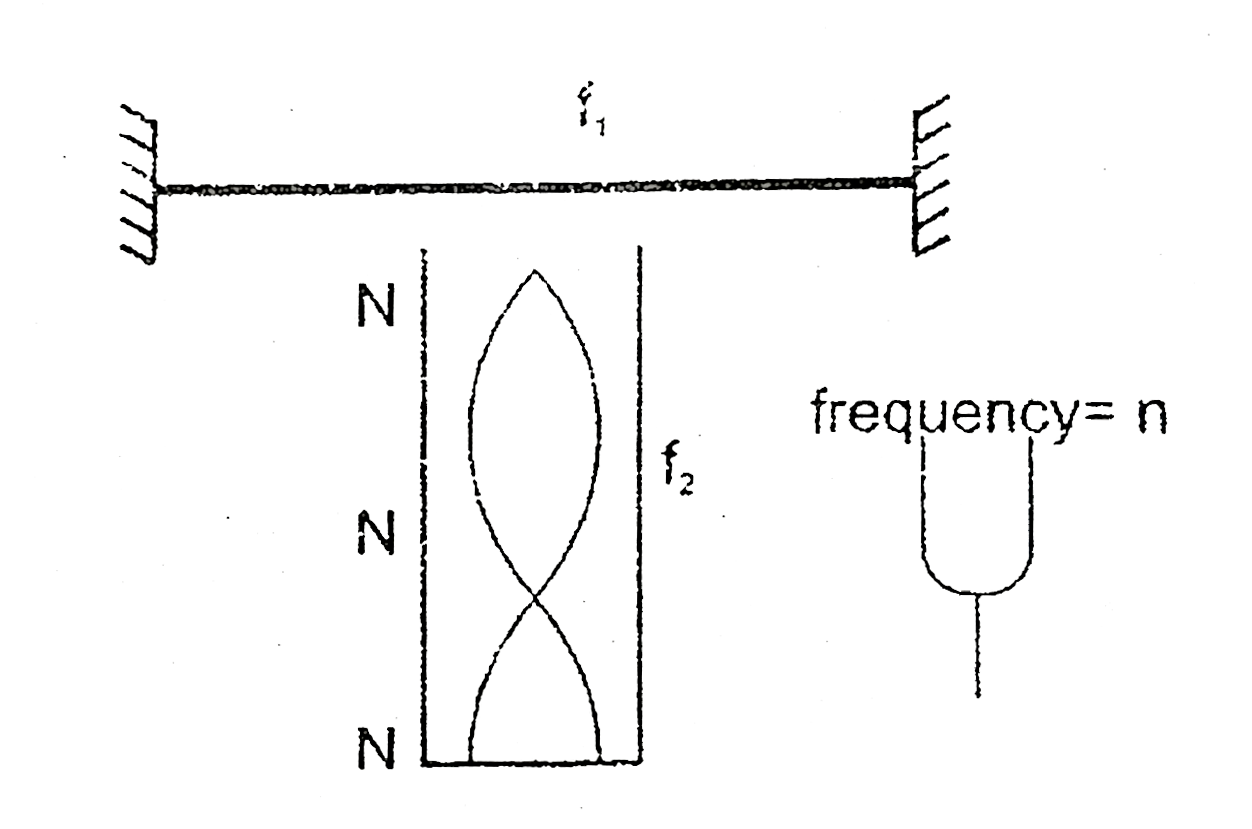
$n = (4 + f_{2})$
$f_{2} = \frac{3 V}{4 l} = \frac{3 \times 340}{4 \times (3 / 4)} = 340$
$n = 344$

|

Updated on:21/07/2023

Class 11 PHYSICS SOUND WAVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A vibrating string of certain length $l$ under a tension $T$ resonates with a maode corresponding to the first overtone (third harmonic) of an air column of length $75 c m$ inside a tube closed at one end. The string also gereates $4$ beats per second when excited along with a tuning fork of frequency $n$ . now when the tension of the string is slightly increased the number of beats reduces $2$ per second. assuming the velocity of sound in air ti be $340 m / s$ , the frequency $n$ of the tuning fork in $H z$ is
A(a) $344$
B(b) $336$
C( c ) $117.3$
D( d ) $109.3$
Question 2 - Select One
A stretched string is in unison with a tuning fork of frequency 392Hz. If the length of the string is decreased by 2% , then the number of beats heard per second will be
A2
B4
C8
D16
Question 3 - Select One
If the air column in a pipe which is closed at one end, is in resonance with a vibrating tuning fork at a frequency 260 Hz, then the length of the air column is
A35.7 cm
B31.7 cm
C12.5 cm
D62.5 cm

RESONANCE-SOUND WAVES-Exercise- 3 PART - I

Home
Ask Doubt
Profile