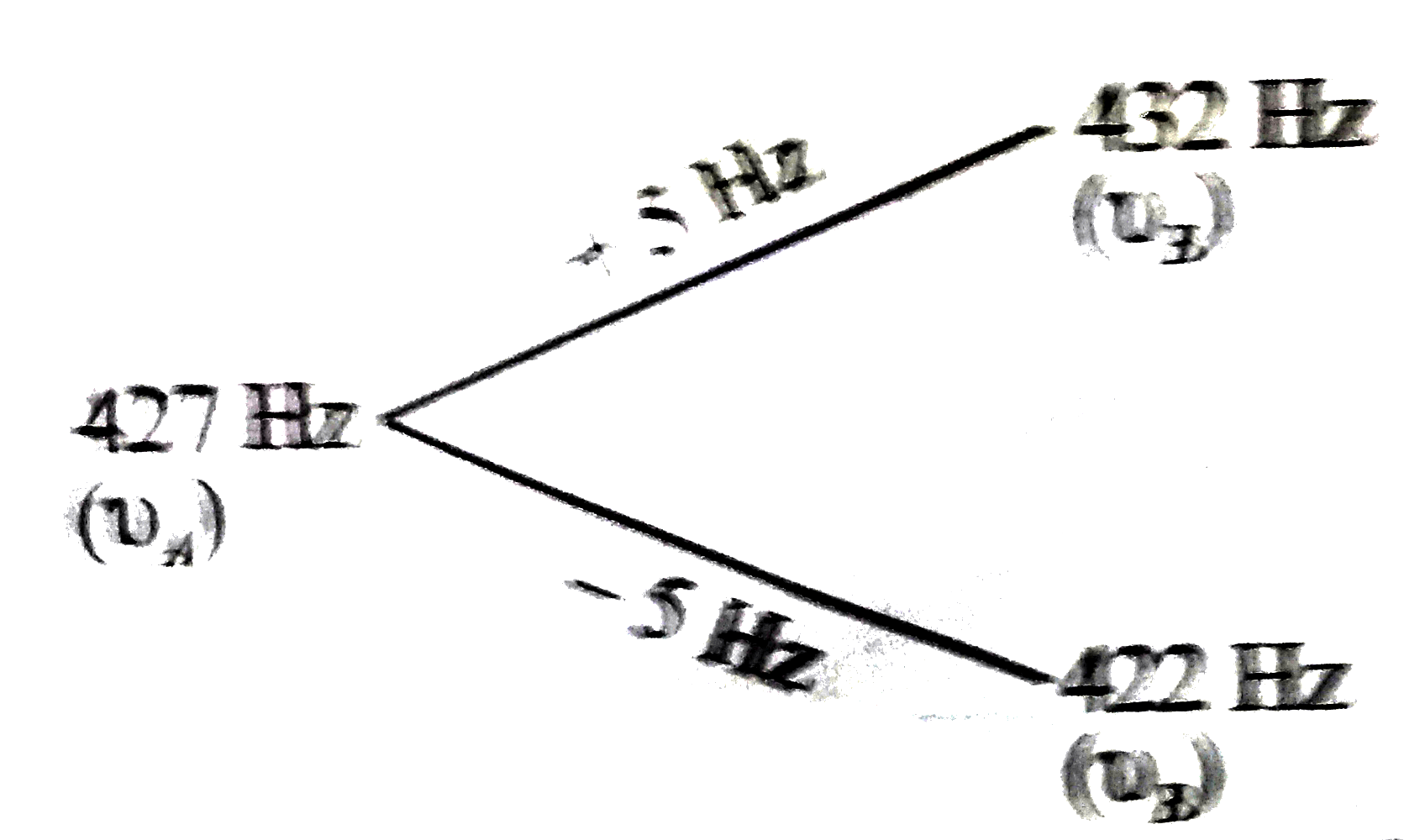
Two sitar strings A and B are slightly out of tune and produce beats of frequency 5 Hz. When the tension in the string B is slightly increased, the beat frequency is found to reduce to 3 Hz. If the frequency of string A is 427 Hz, the original frequency of string B is

A

422 Hz

B

424 Hz

C

430 Hz

D

432 Hz

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

The frequency of string A, υ A = 427 H z
Let original frequency of string B be υ B
∴ υ B = ( υ A ± 5 ) H z = ( 427 ± 5 ) H z
= 432 H z or 422 H z
ocr_image
Increase the tension of a string B, increase its frequency ( v ∝ T )
(i) υ B =432 Hz, a further increase in υ B , increase the beat frequency. But this is not given in the question.
(ii) If υ B = 422 Hz, a further increase in υ B , decrease the beat frequency. This is given in this question.
∴ The original frequency of string B be 422 Hz

Updated on:21/07/2023
|
Class 11PHYSICSTRAVELLING WAVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Two strings X and Y of a sitar produce a beat frequency 4 Hz.When the tension of the string Y is slightly increased the beat frequency is found to be 2 Hz. If the frequency of X is 300 Hz,then the original frequency of Y was

    A296 Hz
    B298 Hz
    C302 Hz
    D304 Hz

  • In a guitar , two strings A and b made of same material are slightly out of tune and produce beats of frequency 6 Hz. when tension in B is slightly decreased, the beat frequency increases to 7 Hz. If the frequency od A is 530 hz, the original frequency of B will be

    A524 Hz
    B536 Hz
    C537 Hz
    D523 Hz

  • Two tuning forks A and B produce 8 beat/s when sounded together. When B is slightly loaded with a wax the beats are reduced to 4 per sec. If the frequency of A is 512 Hz, the frequency of B is

    A508 Hz
    B516 Hz
    C504 Hz
    D520 Hz