Question

Viscosity is the property of fluid by virtue of which fluid offers resistance to deformation under the influence of a tangential force.

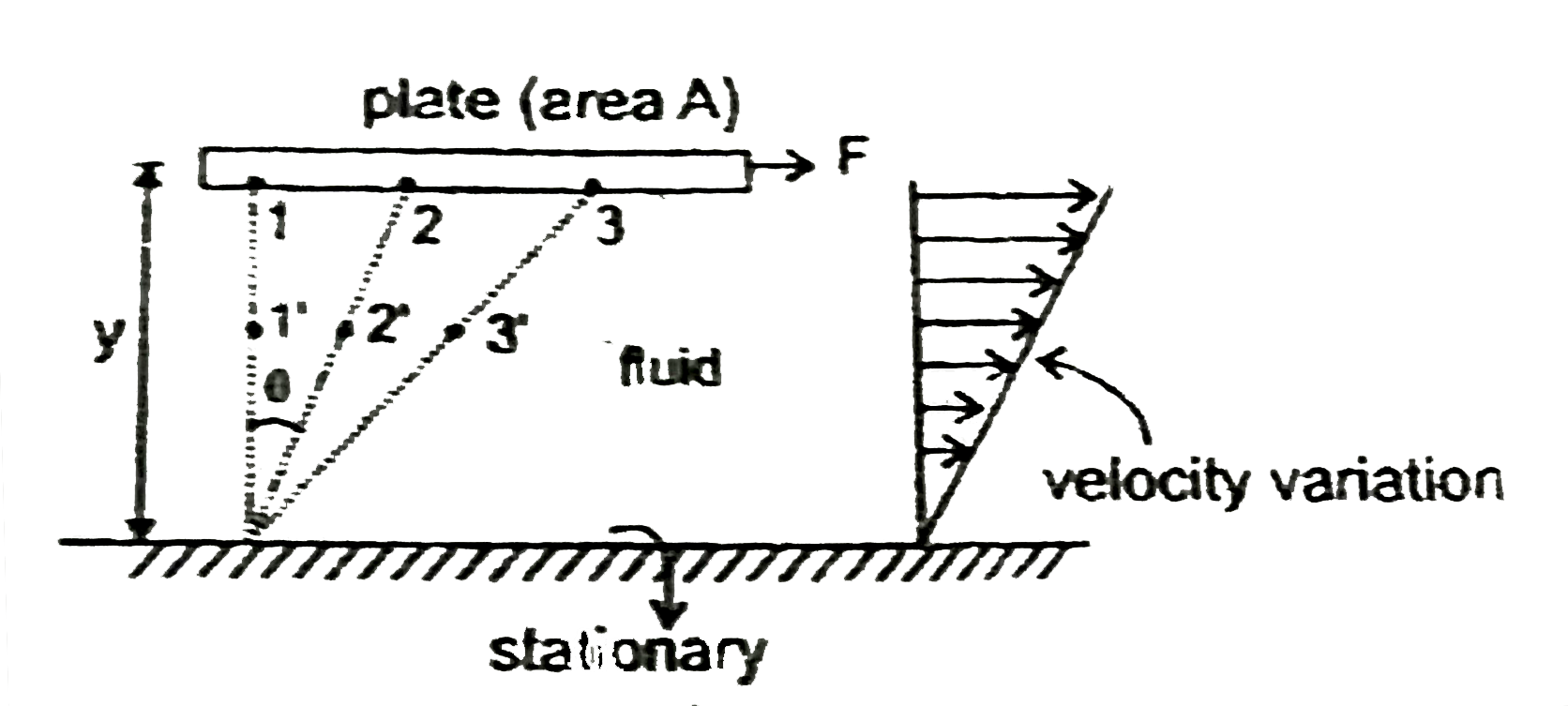
In the given figure as the the plate moves the fluid particle at the surface moves from position $1$ to $2$ and so on, but particles at the bottom boundry remain stationary. if the gap between palte and bottom boundary is small, fluid particles in between plate and bottom moves with velocities as shown by linear velocity distribution curve otherwise the velocity distribution may be parabolic. As per Newton's law of viscity the tangential force is related to time rate of deformation -
$\frac{F}{A}\alpha \frac{d\text{'}\theta }{dt}$ but $y=\frac{d\text{'}\theta }{dt}=u,\frac{d\text{'}\theta }{dt}=\frac{u}{y}$
then $F=\eta A\frac{u}{y},\eta =$ coefficient of viscosity
for non-linear velocity distribution -
$F=\eta A\frac{du}{dy}$
where $\frac{u}{y}$ or $\frac{du}{dy}$ is known as velocity gradiant.
If velocity distribution is given as (parabolic)
$u=c_1{y}^2+c_{2}y+c_3$
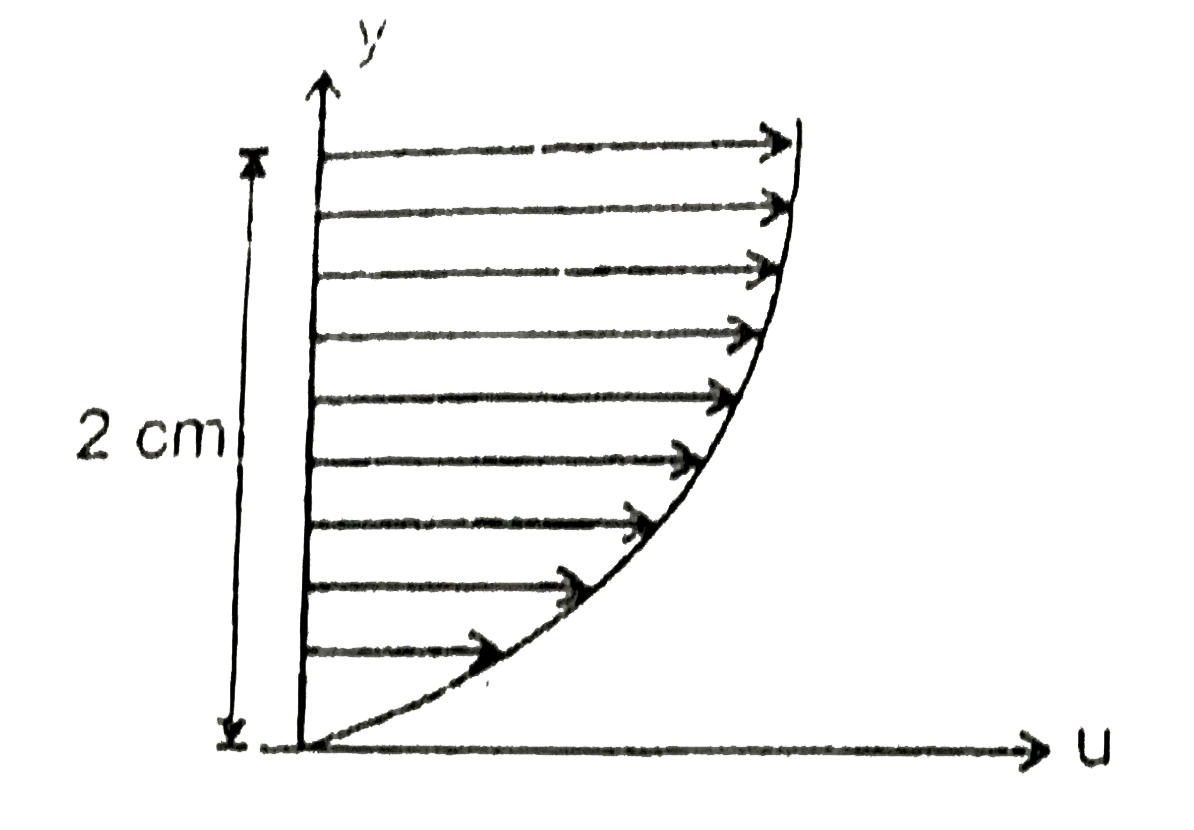For the same force of $2N$ and the speed of the plate $2m/\sec$, the constant $C_1,C_2$ & $C_3$ are

Options

A. `200, 200, 0`
B. `5000, 200, 0`
C. `5000, 0 , 0`
D. `500, 200 , 0`

Answer

C

Explanation

`y = 0 , u = 0 , c_(3) = 0`
`y = 2 cm , u = 2 m//sec`
`2 = C_(1) 4 xx 10^(-4) + C_(2) 2 xx 10^(-2) …(1)`
`(du)/(dy) = 2C_(1)y + 2`
`F = eta A (du)/(dy)`
at `y = 2cm, F = 2 N`
`2 = 10^(-2) xx 1 xx[2 xx 2 xx 10^(-2)C_(1) + C_(2)]`
`4 xx 10^(-4)C_(1) + 10^(-2)C_(2) = 2.......(2)`
`4 xx 10^(-4)C_(1) + 2 xx 10^(-2)C_(2) = 2 .....(1)`
on solving
`C_(2) = 0` & `C_(1) = 5000`