A piston of 796mm diameter and 200mm long works in a cylinder of 800mm diameter as shown in figure. If the annlar spece is flled with a lubicating oil of viscosity 5 centipolses, calculate the constant speed (nearest to integer) of descent of piston in vertical position. The weight of piston and the axial load are 9.8N.

The correct Answer is:8
F=ηAΔVΔZ
9.8=5×10−3π×796×10−3×200×10−3×v2×10−3
v=7.841m/s
Topper's Solved these Questions
- ELASTICITY AND VISCOCITYBOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Exercise- 2 PART - III
11 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Exercise- 3 PART - I
7 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Exercise- 2 PART - I
11 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 92 illustration
2 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise
43 Videos
Similar Questions
A syringe of diameter D = 8 mm and having a nozzie of diameter d = 2 mm is placed horizontally at a height of 1.25 m as shown in the figure . An incompressible and non - viscous liquid is filled in syringe and the piston is moved at speed of 0.25 m/s .Find the range of liquid jet on the ground.

View Solution(i) A conducting cylinder whose inside diameter is 4.00cm contains air compressed by a piston of mass m=13.0kg, which can slides freely in the cylinder shown in the figure. The entire arrangement is immersed in a water bath whose temperature can be controlled. The syetem is initially in equilibrium at temperature t1=20∘C. The initial height of the piston above the bottom of the cylinder is hi=4.00cm.Patm=1×105Nm2 and g=10m/s2.
If the temperature of the water bath is gradually increased to a final temperature tf=100∘C. Find teh height hf of the piston (in cm) at that instant?
(ii) In the above question, if we again start from the initial conditions and the temperature is again gradually raised, and weights are added to the piston to keep its height fixed at hi. Find the value of teh added mass when the final temperature becomes tf=100∘C?

View Solution
Knowledge Check

The hydraulic press shown in the figure is used to raise the mass M through a height of 5.0 mm by performing 500 J of work at the small piston. The diameter of the large piston is 10 cm while that of the smaller one is 2 cm. The mass M isA104kgB103kgC100kgD105kgA syringe of diameter 1 cm having a nozzle of diameter 1 mm, is placed horizontally at a height 5 m from the ground as shown below. An incompressible non-viscous liquid is filled in the syringe and the liquid is compressed by moving the piston at a speed of 0.5 m s−1, the horizontal distance travelled by the liquid jet is(g=10ms−2)
 A12.5 mB25 mC50 mD75 m
A12.5 mB25 mC50 mD75 mAttempt any 4 sub-parts out of 5. Each sub-part carries 1 mark.
Read the following text and answer the following questions on the basis of the same:
Roget's spiral:
Magnetic effects are generally smaller than electric effects. As a consequence, the force between currents is rather small, because of the smallness of the factor μ. Hence, it is difficult to demonstrate attraction or repulsion between currents. Thus, for 5 A current in each wire at a currents. Thus, for 5 A current in each wire at separation of 1 cm, the force per metre would be 5×10−4N, which is about 50 mg weight. It would be like pulling a wire by a string going over a pulley to which a 50 mg weight is attached. The displacement of the wire would be quite unnoticeable. With the use of a soft spring, we can increase the using mercury, we can make the displacement of even a few mm observable very dramatically. You will also need a constant-current supply giving a constant current of about 5 A. Take a soft spring whose natural period of oscillations is about 0.5-1s. Hang it vertically and attach a pointing tip to its lower end, as shown in the figure here. Take some mercury in a dish and adjust the spring such that the tip is just above the mercury surface. Take the DC current source, sonnect one of its terminals to the upper end of the spring and dip the other terminal in mercury. If the tip of the spring touches mercury, the circuit is completed through mercury. Let the DC source be put off to begin with. Let the tip be adjusted so that it just touches the mercury surface. Switch on the constant current supply and watch the fascinating outcome. The spring shrinks with a jerk, the tip comes out of mercury (just by a mm or so), the circuit is broken, the current stop, the spring relaxes and tries to comes back to its original position, the tip again touches mercury establishing a current in the circuit and the cycle continues with tick, tick, tick, ....
The force 10−3 N, is equivalent to:
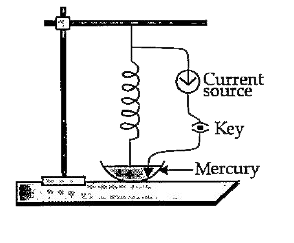 A100 mgB100 gC10 gD10 mg
A100 mgB100 gC10 gD10 mg
2.00 mol of a monatomic ideal gas (U=1.5nRT) is enclosed in an adiabatic, fixed , vertical cylinder fitted with a smooth, light adiabatic piston.the piston is connected to a vertical spring of spring constant 200Nm−1 as shown in .the area of cross section of the cylinder is 20.0cm2. initially, the spring is at its natural length and the temperature of the gas is at its natural length and the temperature of the gas is 300 K. the atmosphere pressure is 100 kPa. the gas is heated sloewly for some time by means of an electric heater so as to move the poston up through 10 cm. find (a) the work done by the gas (b) the final temperature of the gas and (c ) the heat supplied by the heater.

View SolutionAttempt any 4 sub-parts out of 5. Each sub-part carries 1 mark.
Read the following text and answer the following questions on the basis of the same:
Roget's spiral:
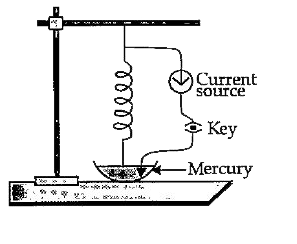
Magnetic effects are generally smaller than electric effects. As a consequence, the force between currents is rather small, because of the smallness of the factor μ. Hence, it is difficult to demonstrate attraction or repulsion between currents. Thus, for 5 A current in each wire at a currents. Thus, for 5 A current in each wire at separation of 1 cm, the force per metre would be 5×10−4N, which is about 50 mg weight. It would be like pulling a wire by a string going over a pulley to which a 50 mg weight is attached. The displacement of the wire would be quite unnoticeable. With the use of a soft spring, we can increase the using mercury, we can make the displacement of even a few mm observable very dramatically. You will also need a constant-current supply giving a constant current of about 5 A. Take a soft spring whose natural period of oscillations is about 0.5-1s. Hang it vertically and attach a pointing tip to its lower end, as shown in the figure here. Take some mercury in a dish and adjust the spring such that the tip is just above the mercury surface. Take the DC current source, sonnect one of its terminals to the upper end of the spring and dip the other terminal in mercury. If the tip of the spring touches mercury, the circuit is completed through mercury. Let the DC source be put off to begin with. Let the tip be adjusted so that it just touches the mercury surface. Switch on the constant current supply and watch the fascinating outcome. The spring shrinks with a jerk, the tip comes out of mercury (just by a mm or so), the circuit is broken, the current stop, the spring relaxes and tries to comes back to its original position, the tip again touches mercury establishing a current in the circuit and the cycle continues with tick, tick, tick, ....
Why the spring shrinks in Roget's spiral?
View SolutionAttempt any 4 sub-parts out of 5. Each sub-part carries 1 mark.
Read the following text and answer the following questions on the basis of the same:
Roget's spiral:
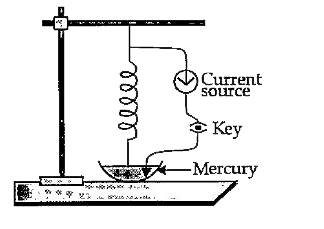
Magnetic effects are generally smaller than electric effects. As a consequence, the force between currents is rather small, because of the smallness of the factor μ. Hence, it is difficult to demonstrate attraction or repulsion between currents. Thus, for 5 A current in each wire at a currents. Thus, for 5 A current in each wire at separation of 1 cm, the force per metre would be 5×10−4N, which is about 50 mg weight. It would be like pulling a wire by a string going over a pulley to which a 50 mg weight is attached. The displacement of the wire would be quite unnoticeable. With the use of a soft spring, we can increase the using mercury, we can make the displacement of even a few mm observable very dramatically. You will also need a constant-current supply giving a constant current of about 5 A. Take a soft spring whose natural period of oscillations is about 0.5-1s. Hang it vertically and attach a pointing tip to its lower end, as shown in the figure here. Take some mercury in a dish and adjust the spring such that the tip is just above the mercury surface. Take the DC current source, sonnect one of its terminals to the upper end of the spring and dip the other terminal in mercury. If the tip of the spring touches mercury, the circuit is completed through mercury. Let the DC source be put off to begin with. Let the tip be adjusted so that it just touches the mercury surface. Switch on the constant current supply and watch the fascinating outcome. The spring shrinks with a jerk, the tip comes out of mercury (just by a mm or so), the circuit is broken, the current stop, the spring relaxes and tries to comes back to its original position, the tip again touches mercury establishing a current in the circuit and the cycle continues with tick, tick, tick, ....
What else can be used instead of mercury in Roget's spiral?
View SolutionAttempt any 4 sub-parts out of 5. Each sub-part carries 1 mark.
Read the following text and answer the following questions on the basis of the same:
Roget's spiral:
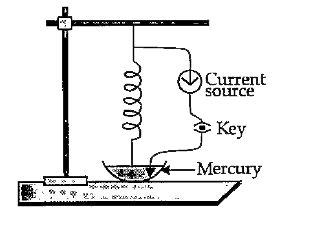
Magnetic effects are generally smaller than electric effects. As a consequence, the force between currents is rather small, because of the smallness of the factor μ. Hence, it is difficult to demonstrate attraction or repulsion between currents. Thus, for 5 A current in each wire at a currents. Thus, for 5 A current in each wire at separation of 1 cm, the force per metre would be 5×10−4N, which is about 50 mg weight. It would be like pulling a wire by a string going over a pulley to which a 50 mg weight is attached. The displacement of the wire would be quite unnoticeable. With the use of a soft spring, we can increase the using mercury, we can make the displacement of even a few mm observable very dramatically. You will also need a constant-current supply giving a constant current of about 5 A. Take a soft spring whose natural period of oscillations is about 0.5-1s. Hang it vertically and attach a pointing tip to its lower end, as shown in the figure here. Take some mercury in a dish and adjust the spring such that the tip is just above the mercury surface. Take the DC current source, sonnect one of its terminals to the upper end of the spring and dip the other terminal in mercury. If the tip of the spring touches mercury, the circuit is completed through mercury. Let the DC source be put off to begin with. Let the tip be adjusted so that it just touches the mercury surface. Switch on the constant current supply and watch the fascinating outcome. The spring shrinks with a jerk, the tip comes out of mercury (just by a mm or so), the circuit is broken, the current stop, the spring relaxes and tries to comes back to its original position, the tip again touches mercury establishing a current in the circuit and the cycle continues with tick, tick, tick, ....
What are main 3 components in a Roget's spiral?
View SolutionAttempt any 4 sub-parts out of 5. Each sub-part carries 1 mark.
Read the following text and answer the following questions on the basis of the same:
Roget's spiral:
Magnetic effects are generally smaller than electric effects. As a consequence, the force between currents is rather small, because of the smallness of the factor μ. Hence, it is difficult to demonstrate attraction or repulsion between currents. Thus, for 5 A current in each wire at a currents. Thus, for 5 A current in each wire at separation of 1 cm, the force per metre would be 5×10−4N, which is about 50 mg weight. It would be like pulling a wire by a string going over a pulley to which a 50 mg weight is attached. The displacement of the wire would be quite unnoticeable. With the use of a soft spring, we can increase the using mercury, we can make the displacement of even a few mm observable very dramatically. You will also need a constant-current supply giving a constant current of about 5 A. Take a soft spring whose natural period of oscillations is about 0.5-1s. Hang it vertically and attach a pointing tip to its lower end, as shown in the figure here. Take some mercury in a dish and adjust the spring such that the tip is just above the mercury surface. Take the DC current source, sonnect one of its terminals to the upper end of the spring and dip the other terminal in mercury. If the tip of the spring touches mercury, the circuit is completed through mercury. Let the DC source be put off to begin with. Let the tip be adjusted so that it just touches the mercury surface. Switch on the constant current supply and watch the fascinating outcome. The spring shrinks with a jerk, the tip comes out of mercury (just by a mm or so), the circuit is broken, the current stop, the spring relaxes and tries to comes back to its original position, the tip again touches mercury establishing a current in the circuit and the cycle continues with tick, tick, tick, ....
Magnetic effects:

View Solution
