In the given figure pulleys and strings are ideal. The time period of (Assume that string remains taut) vertical oscillations of the block is, 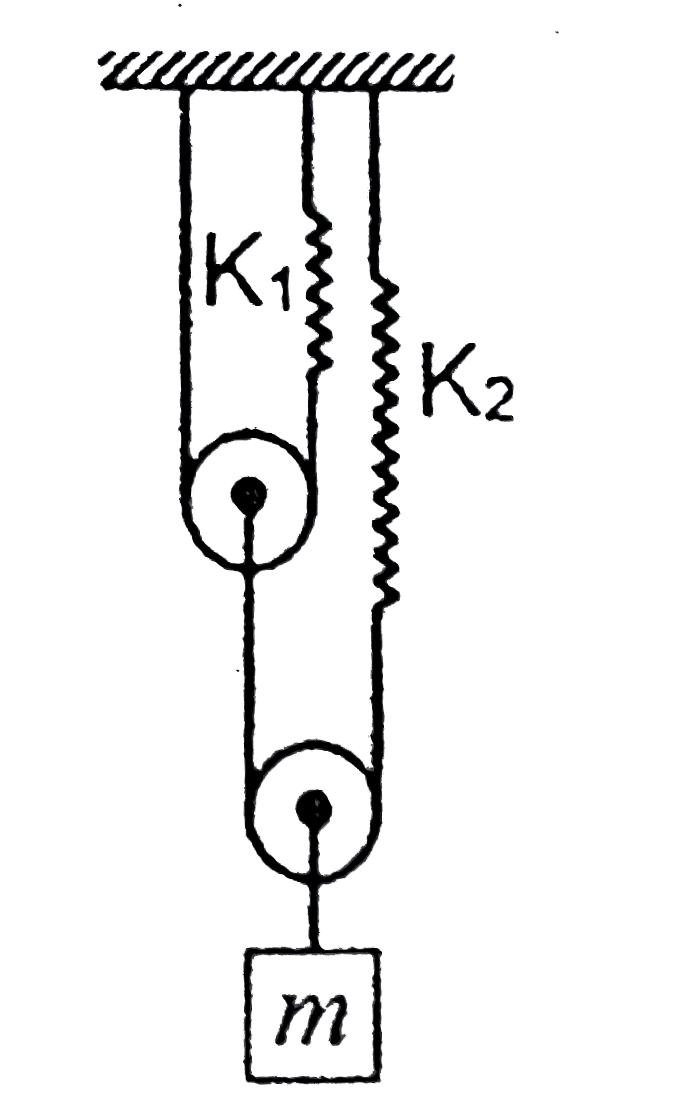
π√m(K2+4K1)K1K2
π2√m(K2+4K1)K1K2
2π√m(K1+K2)K1K2
none of these
The correct Answer is:B
Suppose extension in two spring are x1 and x2
Displacement of block
x=x22+x14
2K1x1=K2x2=F2
1Keq=116K1+14K2,Keq=16K1K24K1+K2
T=2π√m(4K1+K2)16K1K2,T=π2√m(4K1+K2)K1K2
Topper's Solved these Questions
Similar Questions
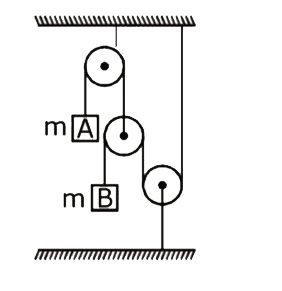
In the arrangement shown, the pulleys and the strings are ideal.The acceleration of the block B is
View SolutionThere is a system of infinite pulleys and springs.Spring constants are in GP as k 2k 4k 8k.........oo as shown in the figure.All the pulleys are massless frictionless and strings are massless and inextensible.Then time period of small oscillations of the block will be (Mass of block is m ). qquad (in ) (i) 2
View Solution
Knowledge Check
In the given figure, pulleys and strings are massless. For equilibrium of the system, the value of is -
 A60∘B30∘C90∘D120∘
A60∘B30∘C90∘D120∘In the given figure, pulleys and strings are massless. For equilibrium of the system, the value of α is -
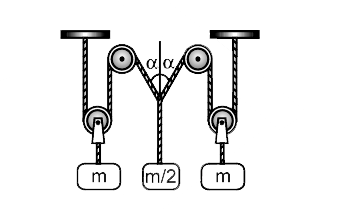 A60∘B30∘C90∘D120∘
A60∘B30∘C90∘D120∘In the shown diagram all pulleys and strings are ideal. The frictional force acting on the 5 block is
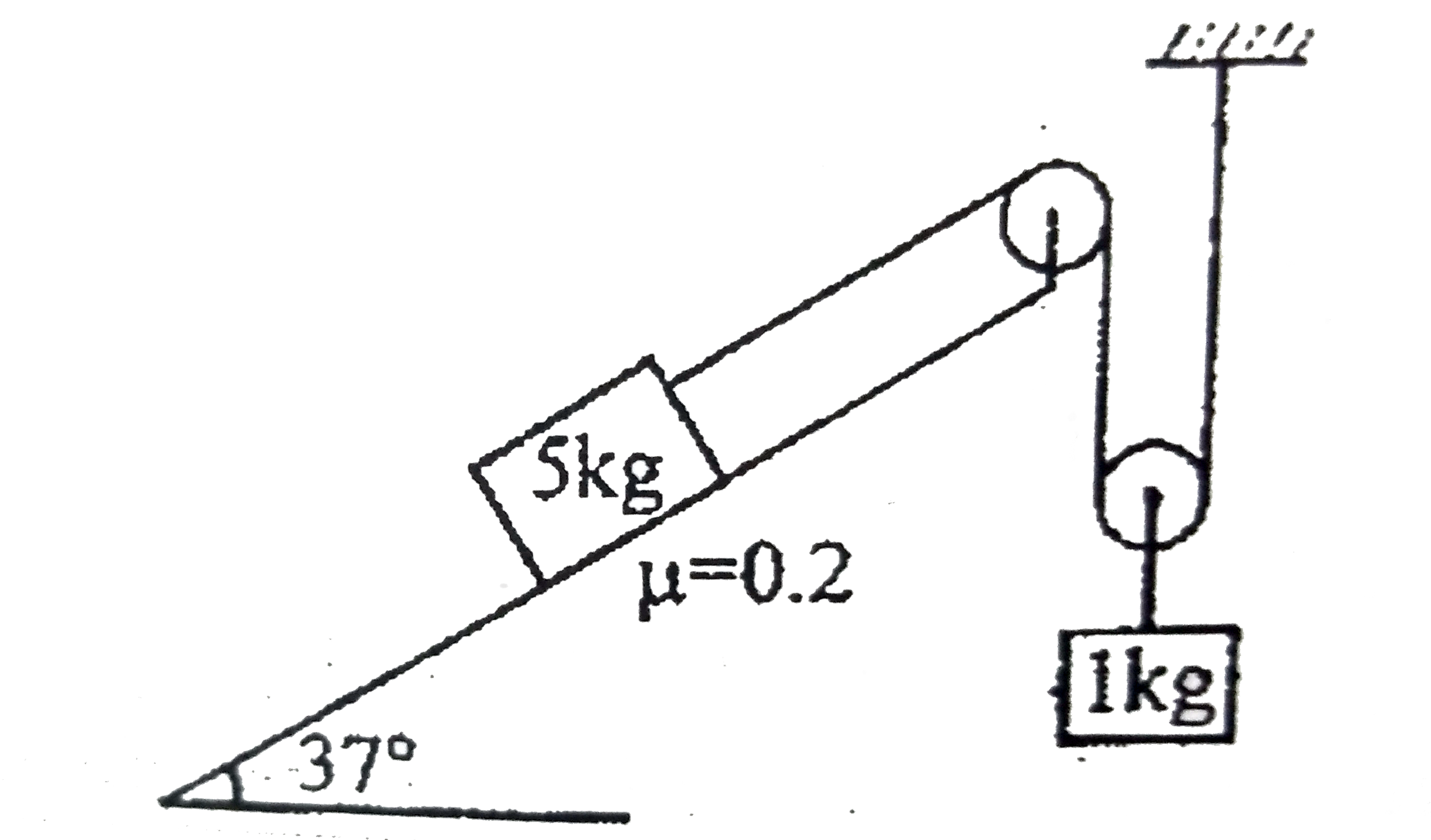 A6NB8NC4ND10N
A6NB8NC4ND10N
Consider a block symmetrically attached to two identical massless springs by means of strings passing over light frictionless pulleys as shown. In the equilibrium position extension in the springs is x0. Find the time period of small vertically oscillations of the blocks.
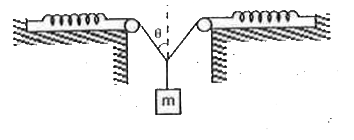
View SolutionThe string, spring and the pulley shown in figure are light. Find the time period of the mass m.

View SolutionIn the arrangement shown, the pulleys and the string are ideal. The acceleration of block B is.

View SolutionIn the shown mass pulley system, pulleys and string are massless. The one end of the string is pulled by the force F = mg. The acceleration of the block will be :

View Solution
In the shown mass pulley system, pulleys and string are massless. The one end of the string is pulleed by the force F=2mg. The acceleration of the block will be
View Solution