Two thin rods of same length l but of different uniform mass per unit length μ1 and μ2 respectively are joined together. The system is rotated on smooth horizontal plane as shown in figure. The tension at the joint will be 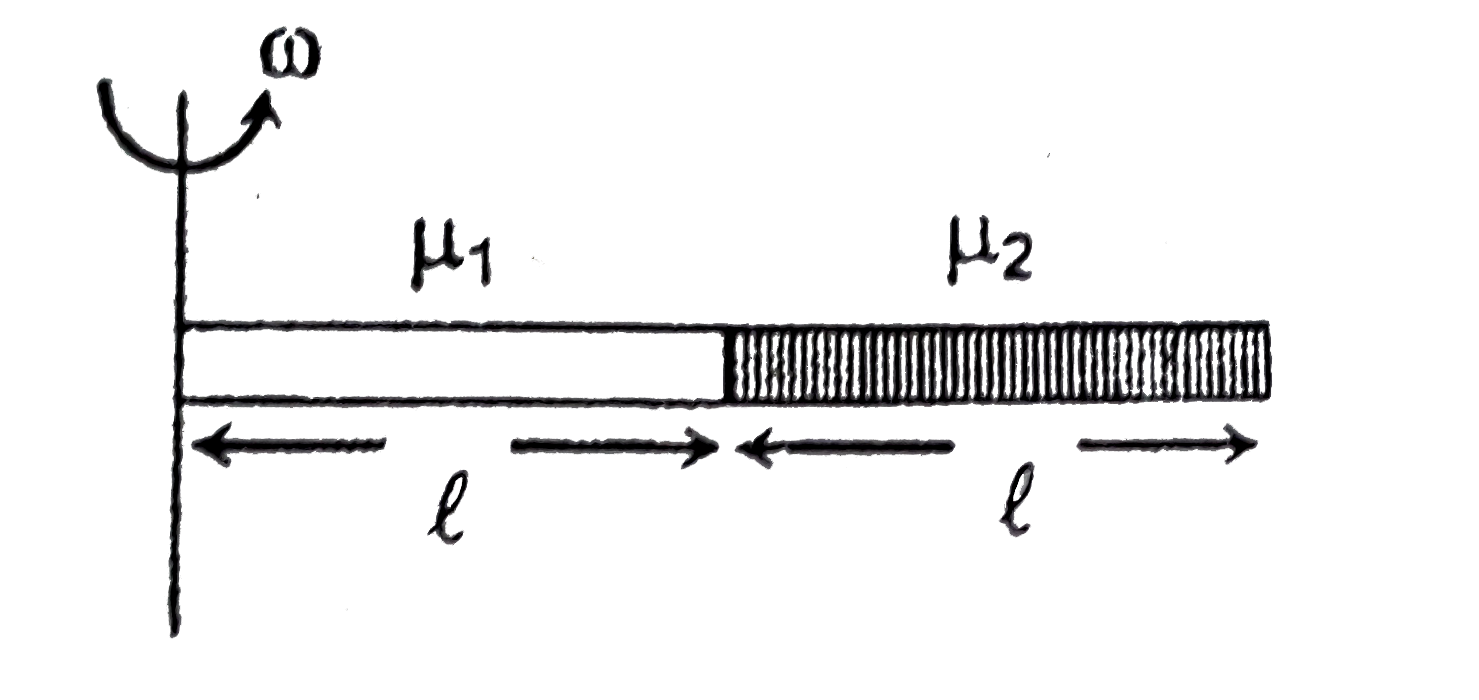
32μ2l2ω2
32(μ1+μ2)l2ω2
32μ1l2ω2
12μ1l2ω2
The correct Answer is:A
The tension at joint is due to force exerted by the root of linear density μ2.
So F=∫2llμ2dxω2x=3μ2ω2l22
Topper's Solved these Questions
Similar Questions
Two strings of the same length but different mass per unit length are used to suspend a rod whose density varies as ρ=ρ0[1+αx] as shown in the figure. The frequency of standing waves produced in the string is in the ratio n:1, when both the strings are vibrating in their fundamental mode. If the mass per unit length of string (l) is μ0, calculate the mass per unit length of the other string.
View SolutionTwo strings under the same tension T but with different values of the mass per unit length μ1 .and μ2 are connected together. A traveling wave pulse of amplitude 1cm is incident on the boundary,going from μ1 to μ2 .If μ2=0.1μ1 ,what is approximately the amplitude of the transmitted pulse?
View Solution
Knowledge Check
A thin circular ring of mass per unit length p and radius r is rotating at an angular speed ω as shown in figure. The tension in the ring is
 Apω2r2/2Bpω2r2Cpω2r2/3DNone
Apω2r2/2Bpω2r2Cpω2r2/3DNoneA thin uniform rod of length L is bent at its mid point as shown in the figure. The distance of the centre of mass from the point O is
 AL2sin(θ2)BL2cos(θ2)CL4sin(θ2)DL4cos(θ2)
AL2sin(θ2)BL2cos(θ2)CL4sin(θ2)DL4cos(θ2)Two identical rods are joined at one of their ends by a pin. Joint is smooth and rods are free to rotate about the joint. Rods are released in vertical plane on a smooth surface as shown in the figure. The displacement of the joint from its initial position to the final position is (i.e. when the rods lie straight on the groun )
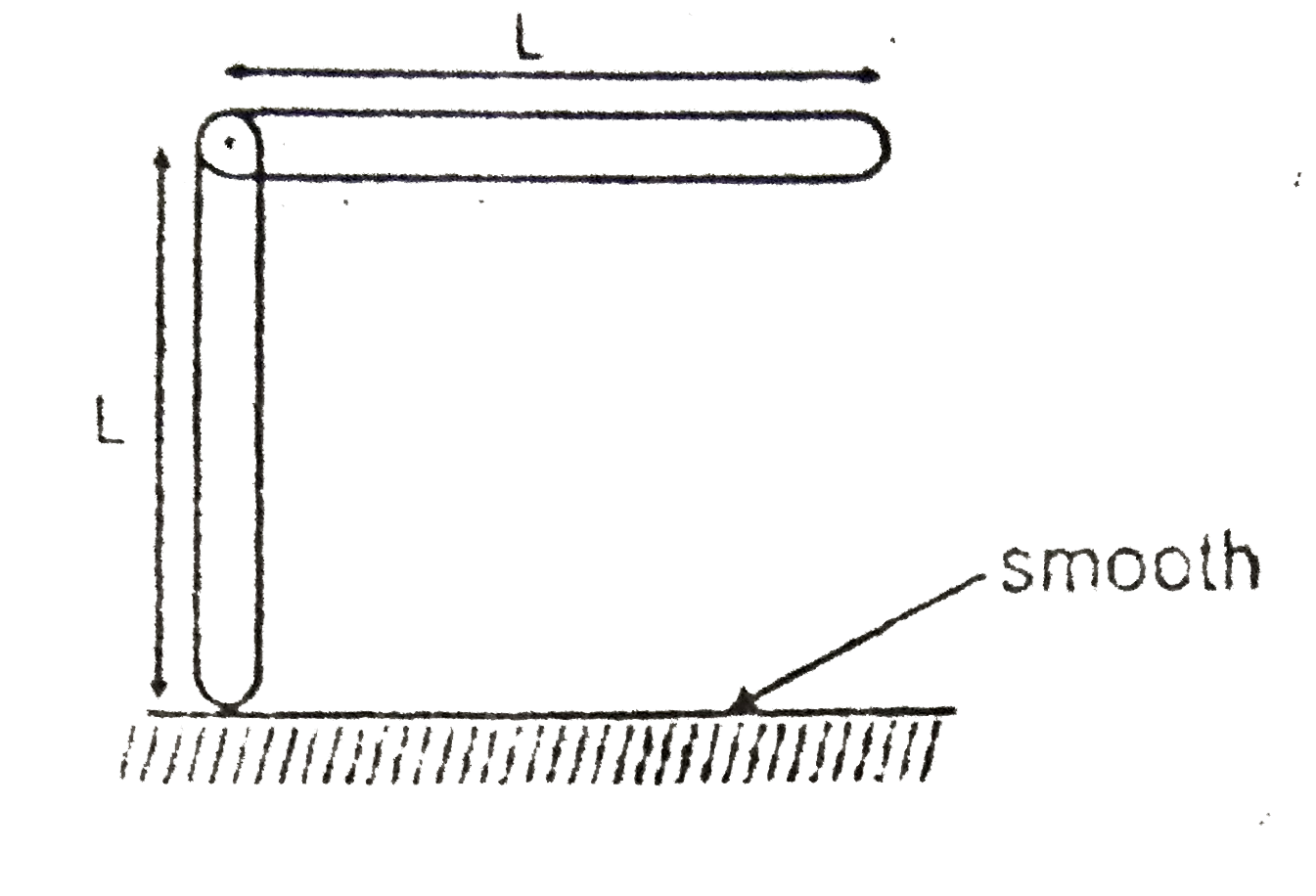 AL4B√174C√15L2Dnone of these
AL4B√174C√15L2Dnone of these
A rod of mass m and length L is non- uniform.The mass of rod per unit length (mu)], varies as "(mu)=bx" ,where b is a constant.The , centre of mass of the ,rod is given by
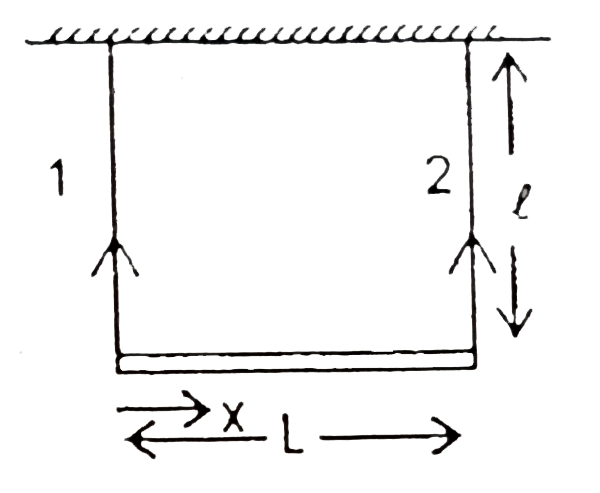
View SolutionA uniform rod of length l and mass m is hung from, strings of equal length from a ceiling as shown in figure. Determine the tensions in the strings?

View SolutionA uniform rope of length 'L and linear density 'μ' is on a smooth horizontal table with a length 'I' lying on the table. The wrok done in pulling the hanging part on to the table is
View SolutionA uniform rod of mass m and length L is suspended with two massless strings as shown in the figure. If the rod is at rest in a horizontal position the ratio of tension in the two strings T1T2 is:

View SolutionA thin uniform copper rod of length l and cross-section area A and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. The elongation of the rod will be
View Solution

