A cart of mass M has a pole on it from which a ball of mass mu hangs from a thin string attached at point P the cart and ball have initial velocity V the cart crashes onto another cart of mass m and sticks to it (figure) If the length of the string is R, the smallest initial velocity (in m//s) for which the ball can go in circles around point P is Neglect friction and assume M, m>>μ Given m=1kgM=2kgR=2m
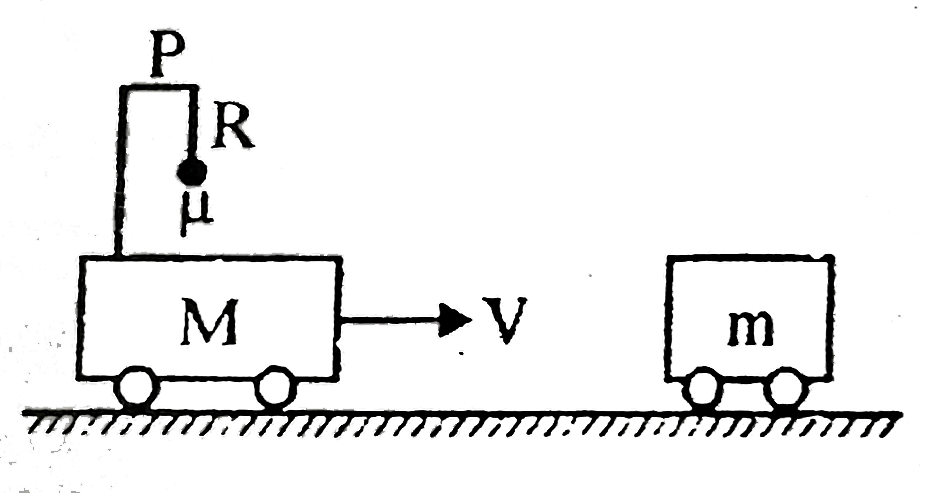
The correct Answer is:0030
As mu lt lt m, M, momemtum conservation
MV=(M+m)V'
gives for the velocity of the two carts after collision,
V'=MVM+m
Consider the circular motion of the ball atop the cart M if it were stationary In at the lowest and highest points the ball has speeds V1 and V2 respectively we have
12μV21=12μV22+2μgR,
μV22R=T+μg
where T is the tension in the string when the ball is at the highest point. The smallest V2 is given by T=0 Hence the smallest V1 is given by
12μV21=12μgR+2μgRi.e.V1=√5gR
With the cart moving, V1 is the velocity of the ball relative to the cart As the ball has initial velocity V and the cart has velocity V' after the collision, the velocity of the ball relative to the cart after the collision is V -V' Hence the smallest V for the ball to go round in a circle after the collision is given by
V−V'=V−MVM+m=√5gRi.e.V=M+mm√5gR
Topper's Solved these Questions
- MASTER PRACTICE PROBLEMBook:BANSALChapter:MASTER PRACTICE PROBLEMExercise:Additional topic
Explore 70 Videos
- MASTER PRACTICE PROBLEMBook:BANSALChapter:MASTER PRACTICE PROBLEMExercise:Multiple objective
Explore 131 Videos
- FLUID MECHANICSBook:BANSALChapter:FLUID MECHANICSExercise:PYQS AIEEE
Explore 10 Videos
- SEMICONDUCTORSBook:BANSALChapter:SEMICONDUCTORSExercise:CBSE Question
Explore 32 Videos
Similar Questions
The manifestation of band structure in solids is due to
View SolutionThe quantity// quantities that does //do not have mass in its// their dimentions (when we take standard 7 quantities as fundmental) is//are:
View SolutionA cylinder of height 20m is completely filled with water. The velocity of effux of water (∈ms−1) through a small hole on the side wall of the cylinder near its bottom is
View SolutionHow does the width of the depletion layer of a p-n junction diode change with decrease in reverse bias?
View SolutionA ball is suspended from the top of a cart by a string of length 1.0m. The cart and the ball are initially moving to the right at constant speed V, as shown in figure I. The cart comes to rest after colliding and sticking to a fixed bumper, as in figure II. The suspended ball swings through a maximum angle 60^@ . The initial speed V is (take g=10(m)/(s^2) )
View SolutionA ball is suspended from the top of a cart by a light string of length 1.0 m. The cart and the ball are initially moving to the right at constant speed V, as shown in figure I. The cart comes to rest after colliding and sticking to a fixed bumper, as in figure II. The suspended ball swings through a maximum angle 60°. The initial speed V is (take g=10m/s2) (neglect friction)
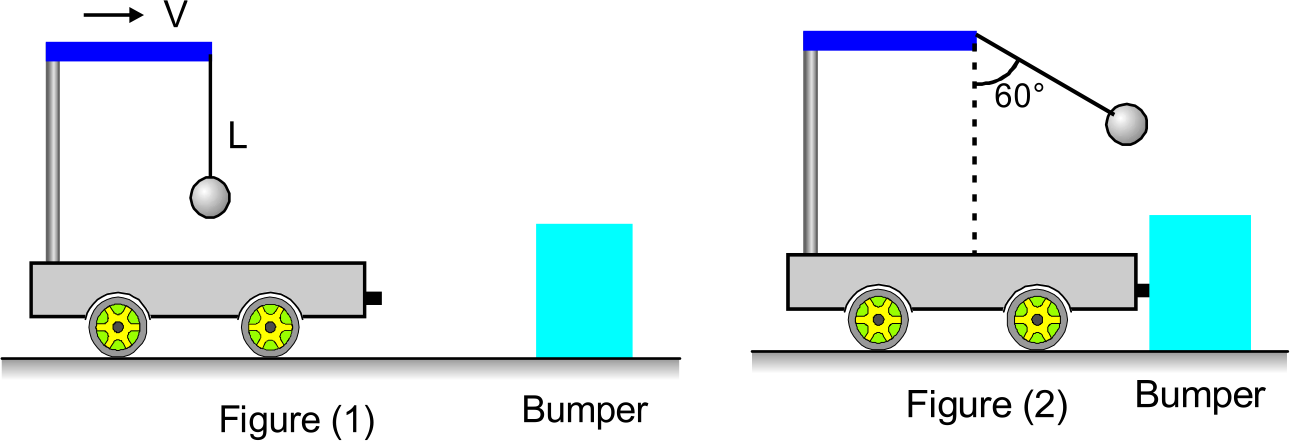
View SolutionA bullet of mass 'm' is fired from a gum of mass M with a (muzzle) velocity u . If the cart on which gun is fixed can move on the smooth horizontal floor as shown Find recoil velocity of the cart
View SolutionA small bob mass 'm' is suspended by a massless string from a cart of the same mass 'm' as shown in the figure. The friction between the cart and horizontal ground is negligible. The bob is given a velocity V_(0) in horizontal direction as shown. The maximum height attained by the bob is , ( initially whole system ( bob + string + cart ) was at rest ) .
View SolutionIn the figure shown a cart moves on a smooth horizontal surface due to an external constant force of magnitude F . The initial mass of the cart is M_(0) and velocity is zero. Sand falls on to the cart with negligible velocity at constant rate mu kg//s and sticks to the cart. The velocity of the cart at time t is :
View SolutionA cart of mass M has a block of mass m in contact with it as shown in the figure-2.133. The coefficient of friction between the block and the cart is mu . What is the minimum acceleration of the cart so that the block m does not fall ?
View SolutionA cart with a mass M=12 kg is connected by a string to a mass of m=200 g. At the initial moment the cart moves to the left along a horizontal plane at a speed v0=7m/s. Distance covered by smooth cart after 5 s is (g=9.8m/s2)
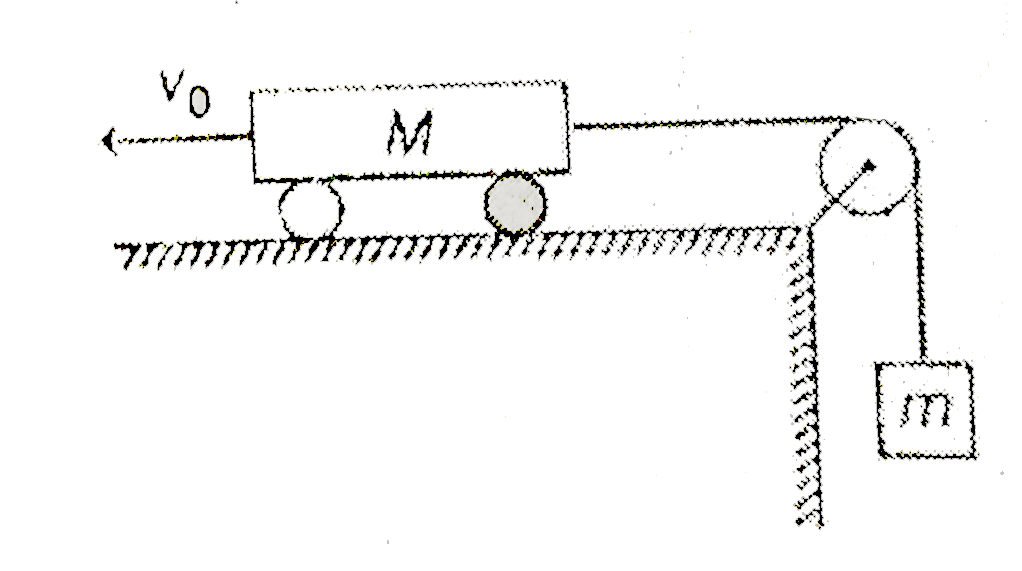
View SolutionA man of mass 80 kg is riding on a small cart of mass 40 kg which is rolling along a level floor at a speed 2 m/s . He is running on the cart , so that his velocity relative to the cart is 3 m/s in the direction opposite to the motion of cart . What is the speed of the centre of the mass of the system ?
View SolutionA ball B is suspended from a string of length l attached to a cart A, which may roll on a frictionless surface. Initially the cart is at rest and the ball is given a horizontal velocity v_(0) . Determine the velocity of B as it reaches the maximum height.
View SolutionA ball B is suspended from a string of length l attached to a cart A, which may roll on a frictionless surface. Initially the cart is at rest and the ball is given a horizontal velocity v0. Determine
the maximum height reached by the ball.
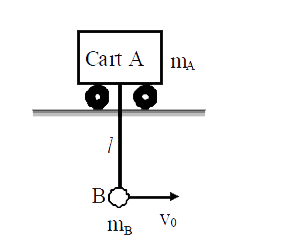
View SolutionA 50.0-kg boy runs at a speed of 10.0 m/s and jumps onto a cart as shown in the figure. The cart is initially at rest. If the speed of the cart with the boy on it is 2.50 m/s, what is the mass of the cart?
View Solution

