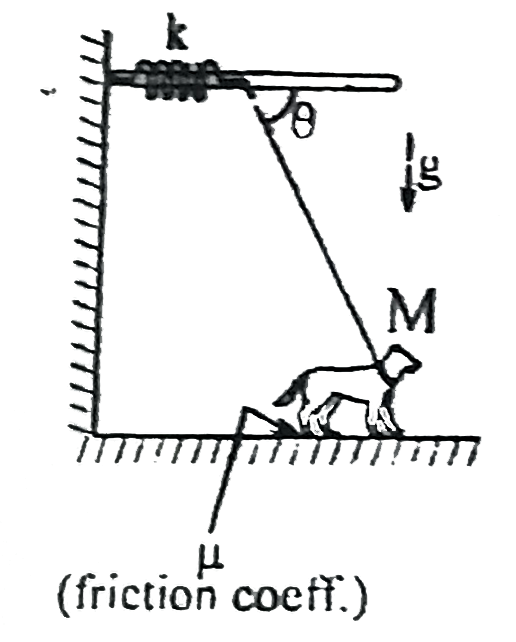
A dog with mass M has its string attached to one end of a spring which runs without friction along a horizontal overhead rod. The other end of the springs is fixed to a wall The spring constant is K. The string is massless and inextensible and it maintains a constant angle θ with the overhead rod, even when the dog moves. There is friction with coefficient mu between the dog and the gound What is the maximum distance (in cm) that the dog moving slowly can stretch the spring beyond its natural length? Use M=30 kg,θ=400N/mandμ=13
The correct Answer is:0020
For the dog, N+Tsinθ−Mg=0 (vertical)
F−Tcosθ=0 (horizontal)
For maximum extension f=μN
For spring Tcosθ−kx=0 (horizontal)
We have four unknows (N,T,F,x) and four equations Solve for T Tcosθ=kx⇒T=kx/cosθ
Substitute for F and solve for N μN−Tcosθ=0⇒N=Tcosθ/μ=kx/μ
Topper's Solved these Questions
- MASTER PRACTICE PROBLEMBook:BANSALChapter:MASTER PRACTICE PROBLEMExercise:Additional topic
Explore 70 Videos
- MASTER PRACTICE PROBLEMBook:BANSALChapter:MASTER PRACTICE PROBLEMExercise:Multiple objective
Explore 131 Videos
- FLUID MECHANICSBook:BANSALChapter:FLUID MECHANICSExercise:PYQS AIEEE
Explore 10 Videos
- SEMICONDUCTORSBook:BANSALChapter:SEMICONDUCTORSExercise:CBSE Question
Explore 32 Videos
Similar Questions
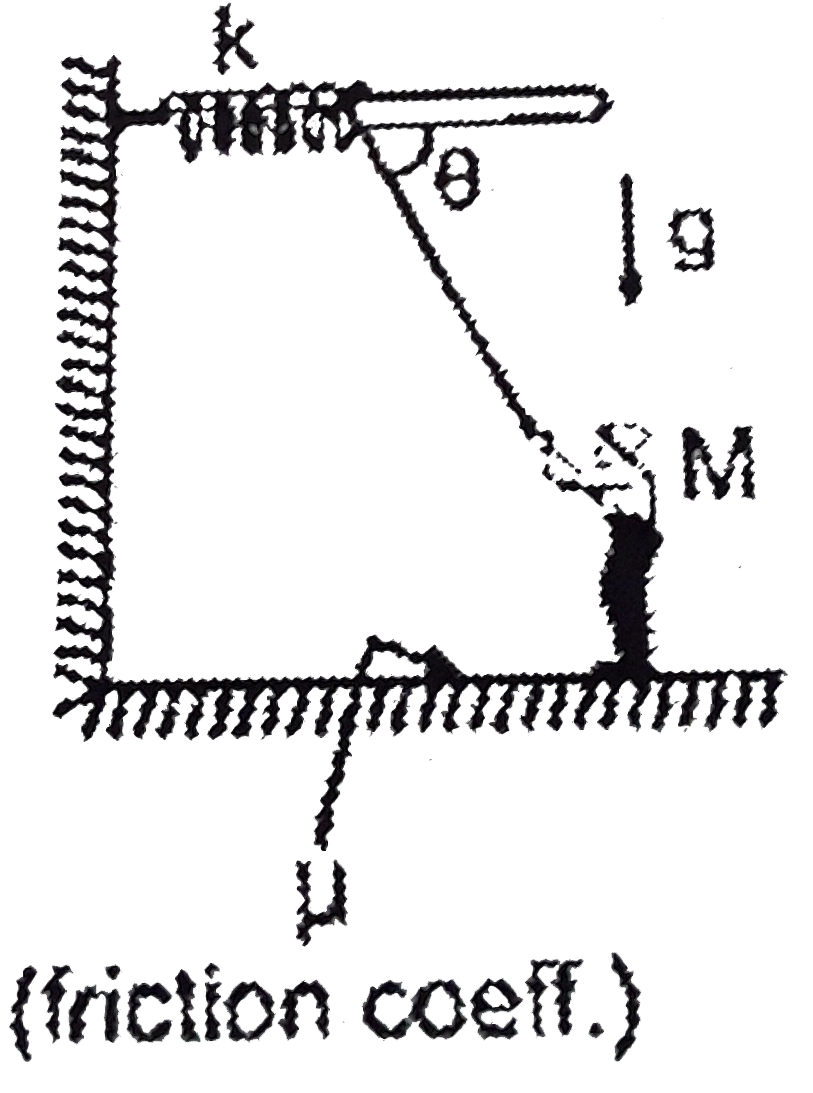
A man with mass M has its string'.attached to one end. of a spring which can move without friction along a horizontal, overhead fixed rod. The other end of the spring is fixed to a, wall. The spring constant is k. The string is massless and inextensible and it maintains a constant angle θ with the, overhead rod, even when the man moves. There is friction, iwith coefficient μ between the man and the ground. What is, the maximum distance (in m ) that the man moving slowly can stretch the spring beyond its natural length?
View SolutionA block of mass m, attached to a spring of spring constant k, oscilltes on a smooth horizontal table. The other end of the spring is fixed to a wall. If it has speed v when the spring is at its naturla lenth, how far will it move on the table before coming to an instantaneous rest?
View Solution
Knowledge Check
A block of mass m, attacted to a string of spring constant k, oscillates on a smooth horizontal table. The other end of the spring is fixed to a wall. The block has a speed v when the spring is at its natural length. Before coming to an instantaneous rest. If the block moves a distance x from the mean position, then
Ax=√mkBa=1v√mkCx=v√mkDx=√mvkA Bead of mass m is attached to one end of a spring of natural length 'R' and spring cosntant 'k=(√3+1)mgR'. The other end of the spring is fixed at point 'A' on a smooth vertical ring of radius 'R' as shown
 Amg/2B√3mgC3√3mgD3√3mg2
Amg/2B√3mgC3√3mgD3√3mg2A bead of mass 'm' is attached to one end of a spring of natural length R & spring constant k=(√3+1)R. The other end of the spring is fixed at point A on a smooth vertical ring of radius R as shown. The normal reaction at B just after it is released to move is
 A√3mgB3√3mgCmg2D3√3mg2
A√3mgB3√3mgCmg2D3√3mg2

A ring of mass m is attached to a horizontal spring of spring constant k and natural length l0. The other end of the spring is fixed and the ring can slide on a horizontal rod as shown. Now the ring is shifted to position B and released Find the speed of the ring when the spring attains its natural length.
View SolutionA small block of mass m=1kg is attached with one end of the spring of force constant K=110Nm−1. Other end of the spring is fixed to a rough plane having coefficient of friction μ=0.2. The spring is kept in its natural length by an inextensible thread ties between its ends as shown in figure. If the thread is burnt, calculate the elongation of the spring when the block attains static equilibrium position.
View SolutionA block of mass M is kept on a rough horizontal surface and is attached with massless spring of force constant k .The minimum constant force applied on the other end of the spring to lift the block is
View SolutionA block of mass 'm' is attached to a spring in natural length of spring constant 'k'. The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.
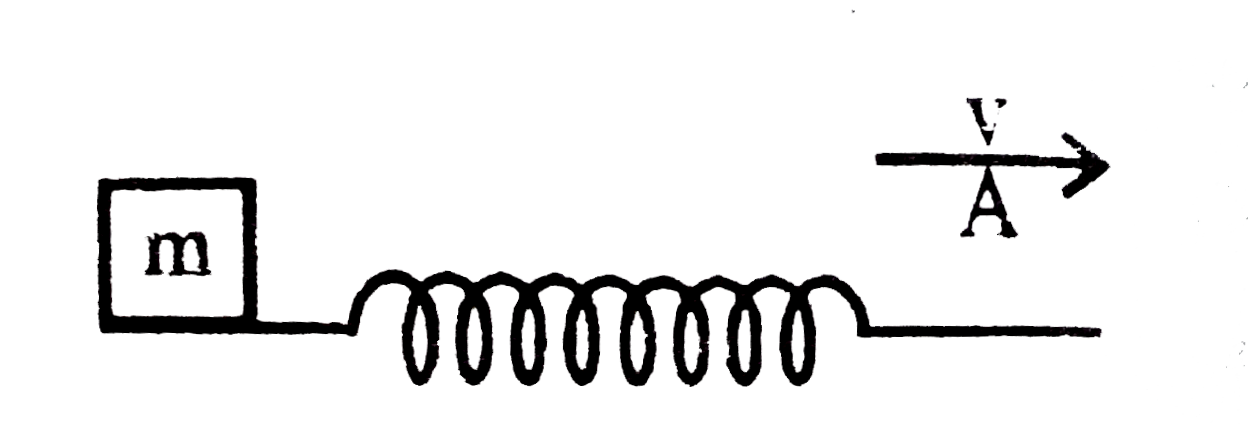
View SolutionAn object of mass m, oscillating on the end of a spring with spring constant k has amplitude A. its maximum speed is
View Solution

