Two students were given a physics problem for finding maximum extension of spring if blocks are imparted velocities v1 & V2 when spring is unstrected.
 By Students A: 12m(v1+v2)2=12kx2
By Students A: 12m(v1+v2)2=12kx2
By Students B: 12mv21+12mv22=12kx2
Student A is correct, Student B is wrong
Student B is correct, Student A is wrong
both are correct
both are wrong
The correct Answer is:D
Velocity of centre of mass is non zero
12(m2)(v1+v2)2=12kx2max
Topper's Solved these Questions
- MASTER PRACTICE PROBLEMBook:BANSALChapter:MASTER PRACTICE PROBLEMExercise:Subjective
Explore 107 Videos
- MASTER PRACTICE PROBLEMBook:BANSALChapter:MASTER PRACTICE PROBLEMExercise:Additional topic
Explore 70 Videos
- MASTER PRACTICE PROBLEMBook:BANSALChapter:MASTER PRACTICE PROBLEMExercise:Reasoning
Explore 75 Videos
- FLUID MECHANICSBook:BANSALChapter:FLUID MECHANICSExercise:PYQS AIEEE
Explore 10 Videos
- SEMICONDUCTORSBook:BANSALChapter:SEMICONDUCTORSExercise:CBSE Question
Explore 32 Videos
Similar Questions
If the mass of a spring, m, is not negligible but small compared to the mass M suspended from it, show that the period of oscillations is given by T=2π√(M+m3)/k, where k is the force constant of the spring.
[Hint: If x and v be the instaneous displacement and velocity of the lower end, then the displacement of an element at a distance z from the fixed end is xz/l and velocity zv/l. The kinetic energy of the spring = (∫t0)12(mdzl)z2v2l2=16mv2
Total energy of the system = 16mv2+12Mv6(2)+12kx2 = a constant. Differentiate anmd find T.]
View SolutionIn the figure block moves downwards with velocity v1, the wedge rightwards with velocity v2. The correct relation between v1 and v2 is
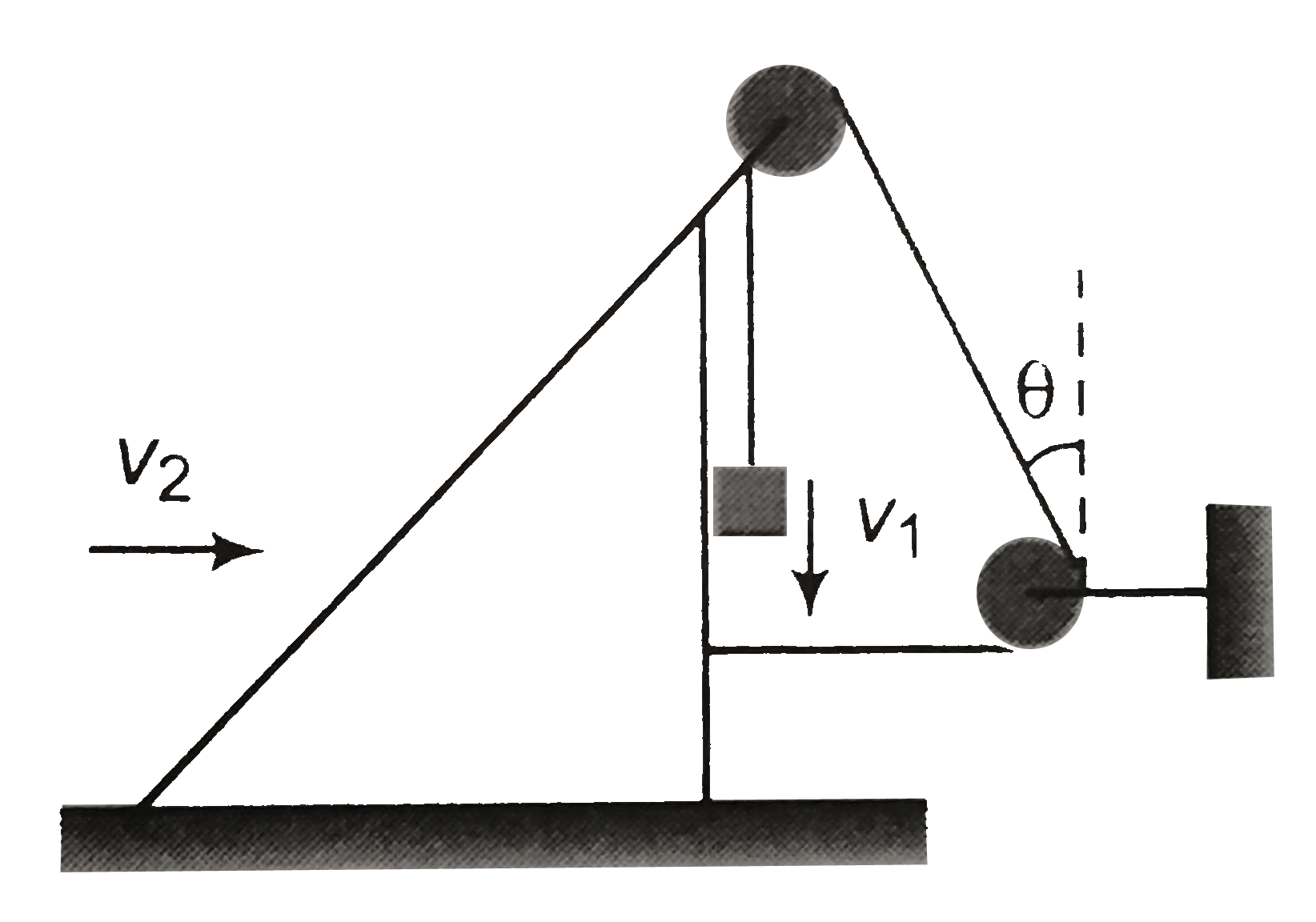
View Solution
Knowledge Check
In fig., blocks A and B move with velocities v1 and v2 along horizontal direction. Find the ratio of v1/v2
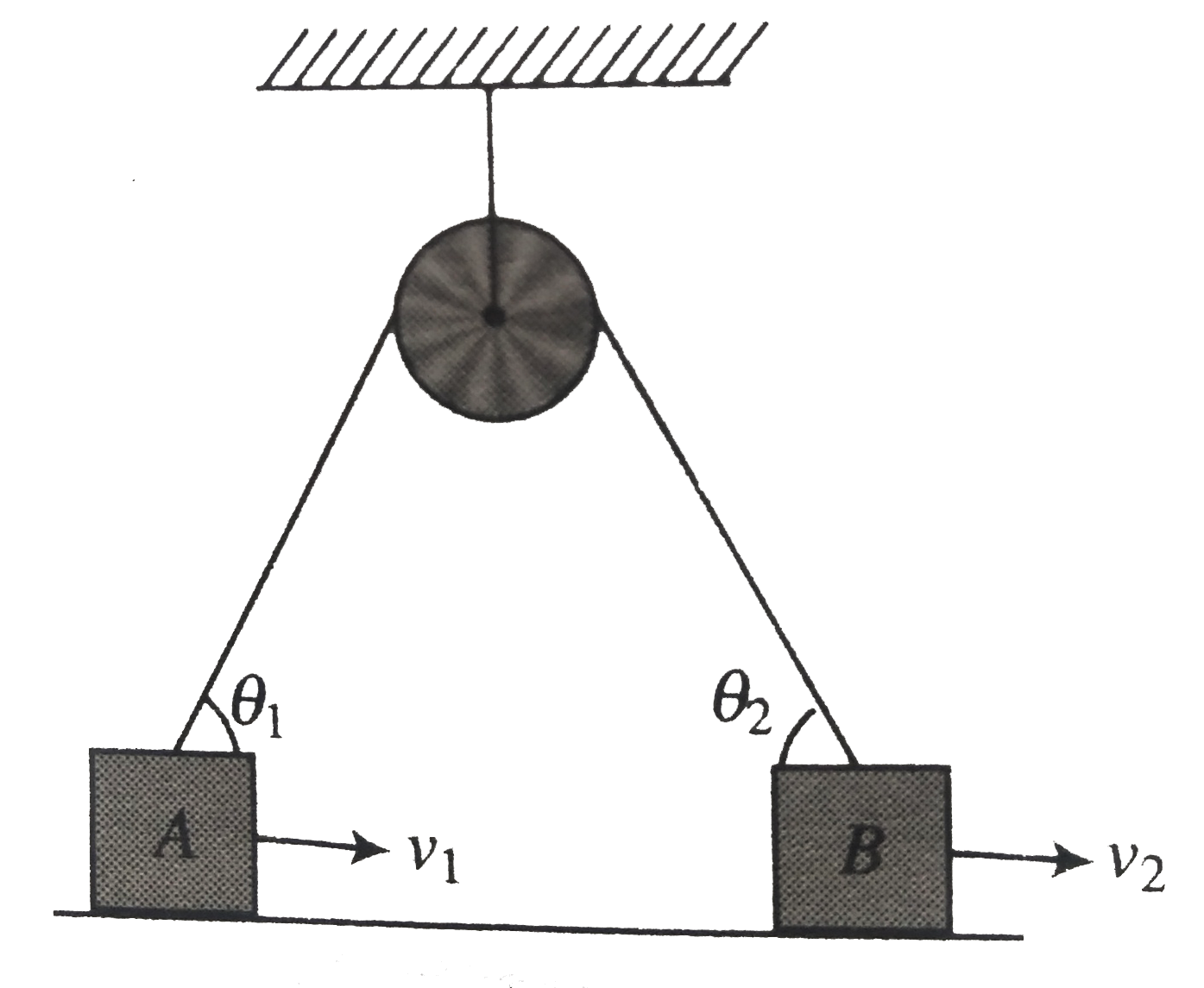 Asinθ1sinθ2Bsinθ2sinθ1Ccosθ2cosθ1Dcosθ1cosθ2
Asinθ1sinθ2Bsinθ2sinθ1Ccosθ2cosθ1Dcosθ1cosθ2In the arrangement shown, blocks A and B connected with an inextensible string move with velocities v1 and v2 along horizontal direction. The ratio of v2v1 is:
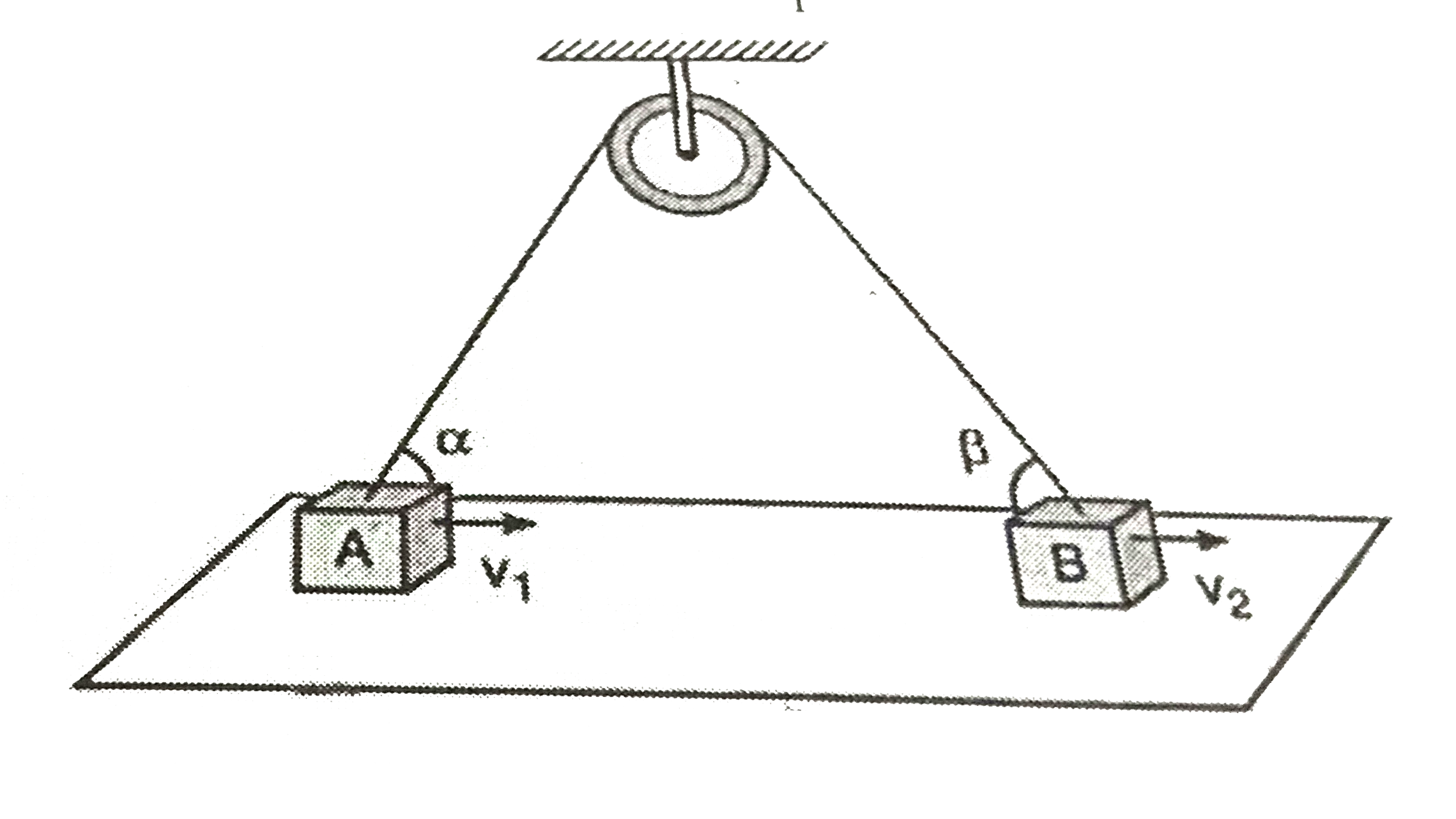 AsinαsinβBsinβsinαCcosβcosαDcosαcosβ
AsinαsinβBsinβsinαCcosβcosαDcosαcosβIn the arrangement shown in figure the ratio of velocity V1&V2 of block (1)&(2) is
 AV1V2=2cotθBV1V2=sinθ2CV1V2=2sinθDnone
AV1V2=2cotθBV1V2=sinθ2CV1V2=2sinθDnone
A stationary partical explodes into two partical of a masses m1andm2 which move in opposite direction with velocities v1andv2. The ratio of their kinetic energies E1/E2 is
View SolutionTwo cars of same mass are moving with velocities v1andv2 respectively. If they are stopped by supplying same breaking power in time t1andt2 respectively then v1v2 is
View SolutionA stationary partical explodes into two partical of a masses m1andm2 which move in opposite direction with velocities v1andv2. The ratio of their kinetic energies E1/E2 is
View SolutionThe ratio of de broglie wavelength of electron accelerated through potentials V1 and V2 is 1:2 the ratio of potentials V1:V2 is
View SolutionGraphical soluton of a two body head on collision
A block A of mass m moving with a uniform velocity v0 strikes another identical block B kept at rest on a horizontal smooth surface as shown in the figure (i). We can conserve linear momentum.
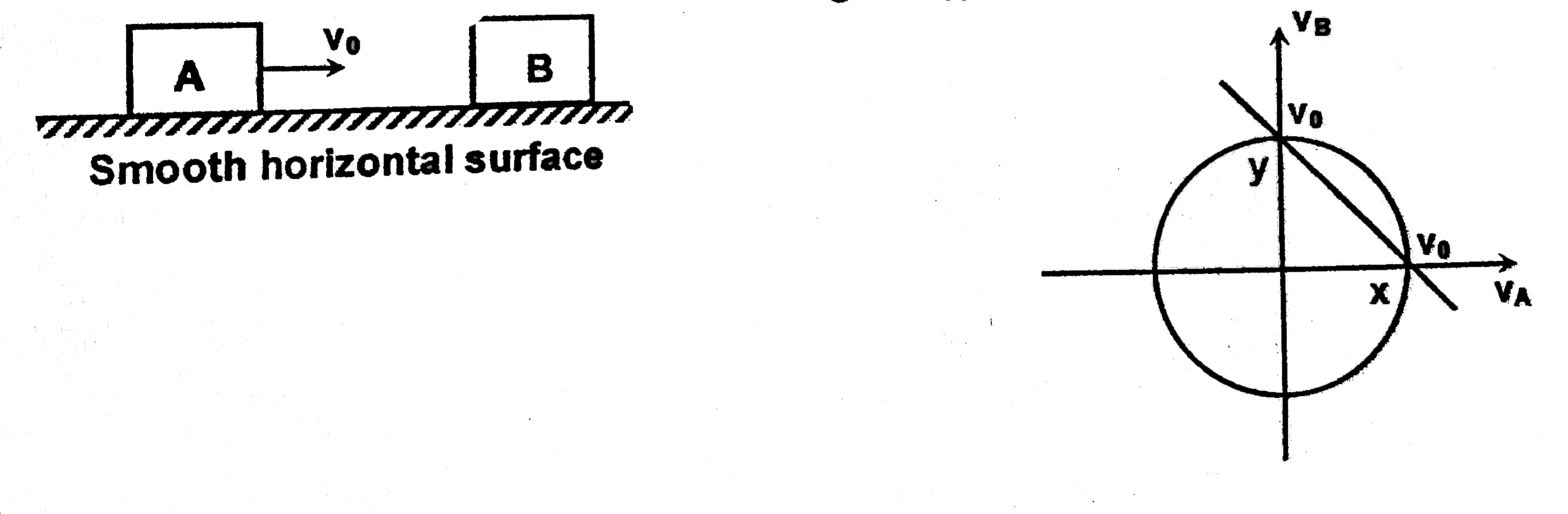
So mv0=mvAmvB (vA and vB are the velocities of the blocks after collision)
∴v0=vA+vB.........(i)
If the collision is perfectly elastic
12mv20=12mv2A+12mv2B
⇒v20=v2A+v2B......(ii)
Both the above equation (i) and (ii) are plotted on vA−vB plane as shown in figure (ii). This plot can be used to find the unknowns vA and vB.
For example the solution of the situation in figure (i) is vA=0,vB=v0 (point y in the plot)
Because vA=v0,vB=0 (point x in the plot) is not physically possible.
In a situation block A is moving with velocity 2m/s an strikes another identical block B kept at rest. The vA−vB plot for the situation is shown. m and l are the intersection points whose vA,vB coordinaes are given in the figure. The coefficient of restitution of the collision is

View Solution

