Question

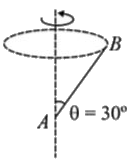
Figure shows a rigid body that is mirror symmetric about a plane and rotates about an axis perpendicular to that plane.

Statement-1: Angular momentum of above mentioned rigid body can be expressed by $\overrightarrow{L}=\overrightarrow{I\omega }$ where I is moment of inertia about rotation axis.
Statement-2: $\overrightarrow{–}\left(L\right)=I\overrightarrow{\omega }$ can be applied only for those rigid bodies that have rotational symmetry about an axis and rotate about that symmetry axis.

Options

A. Statement-1 is true, statement-2 is true and statement-2 is correct explanation for statement-1.
B. Statement-1 is true, statement-2 is true and statement-2 is NOT the correct explanation for statement-1.
C. Statement-1 is true, statement-2 is false.
D. Statement -1 is false, statement -2 is true.

Answer

C

Explanation

`vec(L)=vec(I)omega` can be applied about any axis