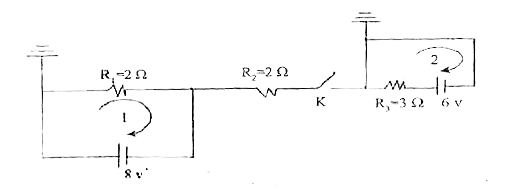
Refer to the circuit diagram and the corresponding graphs. The current rises when key K is pressed. With R=R1andL=L1 the rise of current is shown by curve(1), while curve(2) shows the rise of current when R=R2andL=L2. The maximum current is same for both curves, then:

A
R1=R2,L1>L2
B
R1>R2,L1=L2
C
R1>R2,L1<L2
D
R1=R2,L1<L2
Video Solution
Text Solution
The correct Answer is:D
Consider the expression for the current rising exponentially in the LR circuit. The time constant is (L/R). In this case the curve (1) is rising faster than curve (2) indicating that (L1/R1)<(L2/R2). However, in both the cases the maximum current is the same and equal to (V/R1)or(V/R2). which means R1=R2
|
Topper's Solved these Questions
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Comphrehension
134 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Reasoning
75 Videos
- FLUID MECHANICSBOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE
10 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
Knowledge Check
The current in the series L-C-R circuit is
Ai=imsin(ωt+ϕ)Bi=vm√R2+(Xc−XL)2sin(ωt+ϕ)Ci=2imcos(ωt+ϕ)DBoth (a) and (b)Two inductors L1 and L2 are connected in parallel and a time varying current flows as shown.
the ratio of current i1/i2
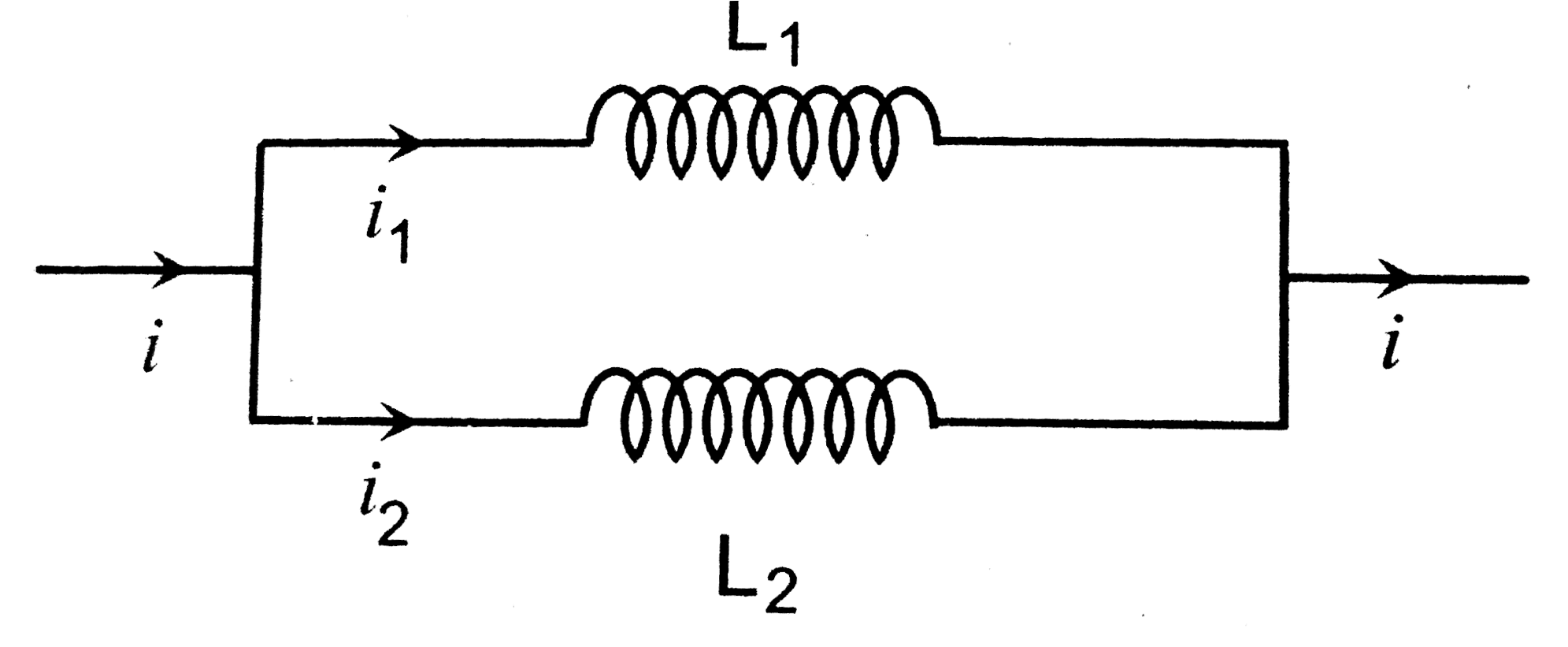 AL1/L2BL2/L1CL21(L1+L22)DL22(L1+L22)
AL1/L2BL2/L1CL21(L1+L22)DL22(L1+L22)Asseration: The growth of current in (RL) circuite is uniform.
Reason: Inductor (L) opposes the growth of current.AIf both asseration and reason are true and reason is the correct explanation of assertion.BIf both asseration and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf assertion is false but reason is true.
Growth and decay of current In L-R Circuit
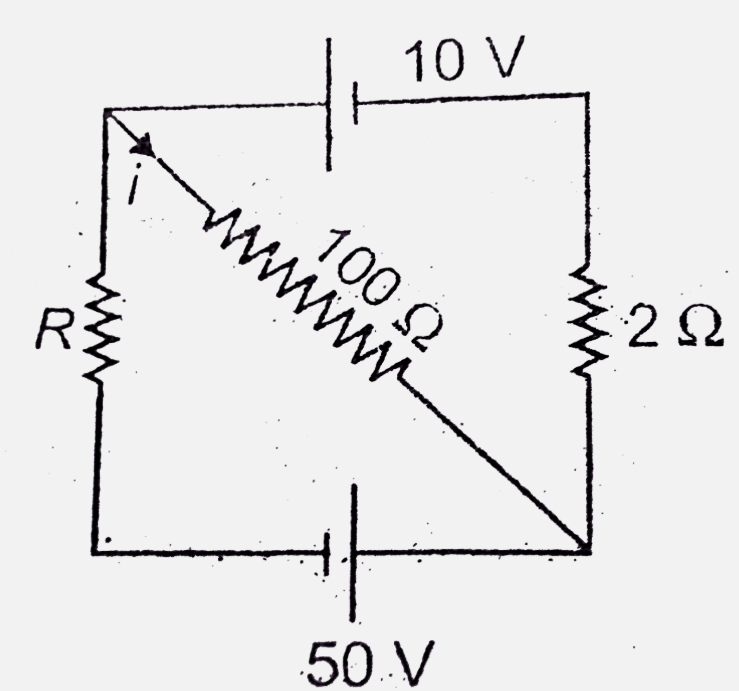
View SolutionA series L-C-R circuit is given in figure . The current through the circuit is
View SolutionIn the circuit diagram shown in Figure, R=10Ω,L=l5H,E=20v,i=2A. This current is decreasing at a rate of −1.0A/s. Find Vab at this instant.

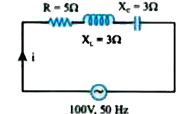
View SolutionIn the circuit shown in the figure XL=XC2)=R the peck value current i0 is
View SolutionDuring current growth in an L-R circuit the time constant is the time in which the magnitude of current becomes
View Solution