A solid spere of mass M and radius R is kept on rough surface the velocities of air (density p) around the sphere are as shown in figure Assuming R to be small and M=4πρR2gkg what is the minimum value of coefficient of friction so that the sphere starts pure rolling? (Assume force due to pressure difference is acting on centre of mass of the sphere)

0.25
0.50
0.75
1.0
The correct Answer is:A
force due to pressure difference is F=12ρπR2(v22_v21)=7ρπR22
Now F−f=Ma
fR=25MR2×aR
⇒f=25Ma⇒f=27F=ρπR2⇒μmg=πρR2
⇒μ=πρR2mg=14=0.25
Topper's Solved these Questions
- MASTER PRACTICE PROBLEMBook:BANSALChapter:MASTER PRACTICE PROBLEMExercise:Comphrehension
Explore 134 Videos
- MASTER PRACTICE PROBLEMBook:BANSALChapter:MASTER PRACTICE PROBLEMExercise:Reasoning
Explore 75 Videos
- FLUID MECHANICSBook:BANSALChapter:FLUID MECHANICSExercise:PYQS AIEEE
Explore 10 Videos
- SEMICONDUCTORSBook:BANSALChapter:SEMICONDUCTORSExercise:CBSE Question
Explore 32 Videos
Similar Questions

A solid sphere of mass M and radius R is hit by a cue at a height h above the centre C. for what value of h the sphere will rool without slipping ?
View Solution
A solid sphere of mass m and radius R is rolling without slipping as shown in figure. Find angular momentum of the sphere about z-axis.
View Solution
Knowledge Check
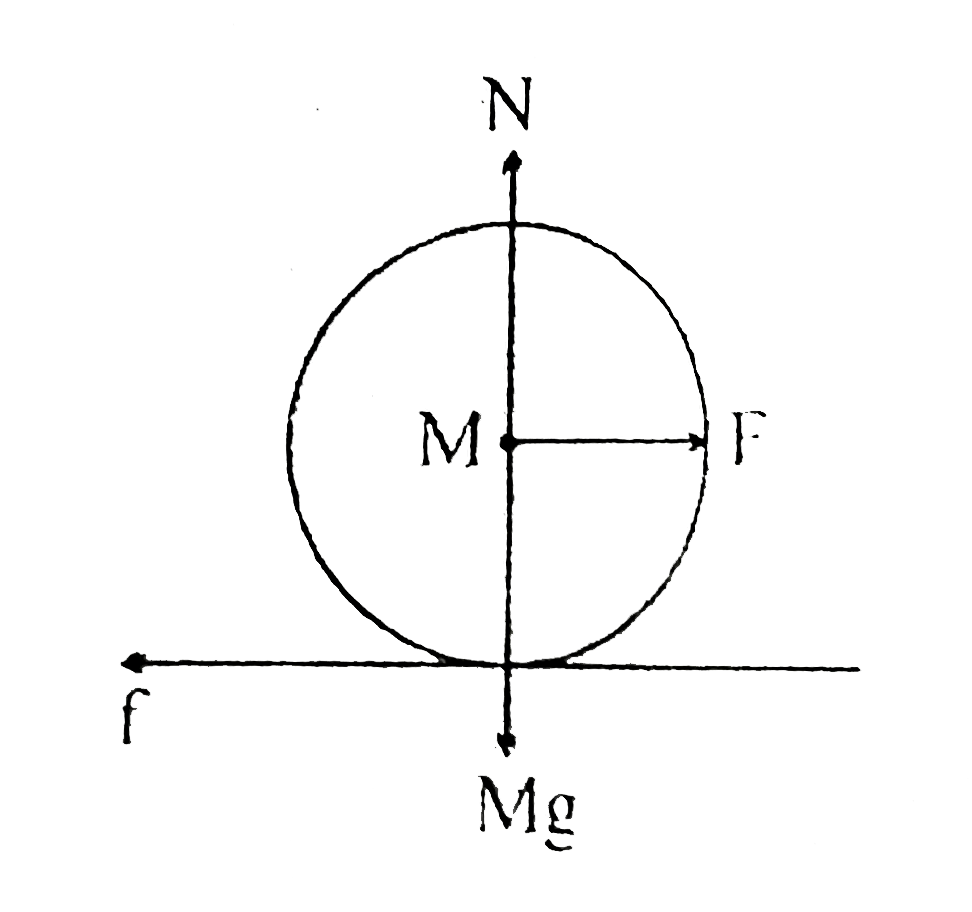
A solid sphere of mass M and radius R is pulled horizontally on a rough surface as shown in Fig. Choose the incorrect alternatives.
 AThe magnitude of the frictional force isF/3.BThe frictional force on the sphere acts forward.CThe acceleration of the centre of mass is 2F/3MDThe acceleration of the centre of mass is F/M.
AThe magnitude of the frictional force isF/3.BThe frictional force on the sphere acts forward.CThe acceleration of the centre of mass is 2F/3MDThe acceleration of the centre of mass is F/M.A solid cylinder of mass M and radius R pure rolls on a rough surface as shown in the figure. Choose the correct alternative (s).
 AThe acceleration of the centre of mass is FMBThe acceleration of the centre of mass is 23FMCThe friction force on the cylinder acts backwardDThe magnitude of the friction force is F3
AThe acceleration of the centre of mass is FMBThe acceleration of the centre of mass is 23FMCThe friction force on the cylinder acts backwardDThe magnitude of the friction force is F3A uniform solid sphere of mass M and radius R is lying on a rough horizonal plane. A constant force F=4Mg acts vertically downwards at point P such that the line OP makes an angle of 60∘ with the horizontal as shown in the figure. The minimum value of the coefficient of friction μ so that sphere performs pure rolling, is
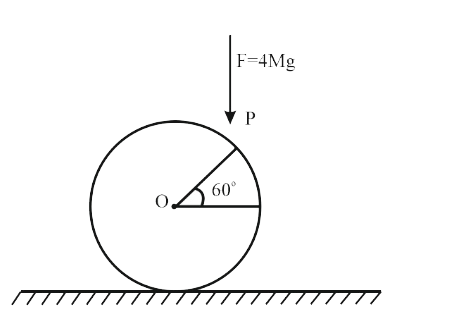 A37B47C27D25
A37B47C27D25
A solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.

A Horizontal force F is applied on the plank. What is the maximum value of F, if μ is coefficient of friction between sphere movment and plank and there is no slipping ?
View SolutionA solid sphere of mass M and radius R is pulled by a force F as shown in figure . If the sphere does not slip over the surface , then frictional force acting on the sphere is

View SolutionA solid sphere of mass m and radius R is on a rough surface as shown in figure. Two forces having magnitude 2F and F are applied as shown. If the sphere perfors pure rolling along right direction, then frictional force acting on the sphere is
_PHY_211_Q01.png)
View SolutionA solid sphere of mass M and radius R is placed on a smooth horizontal surface. It is given a horizontal impulse J at a height h above the centre of mass and sphere starts rolling then, the value of h and speed of centre of mass are –
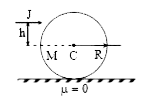
View SolutionA solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that vc.m.=v0.
View Solution
