If 12|x|=1and|y|=x+1, then y2 could be
2
3
4
9
The correct Answer is:D
To solve the problem step by step, we will start from the given equations and derive the possible values of y2.
Step 1: Solve for x
We start with the equation:
12|x|=1
To eliminate the fraction, we multiply both sides by 2:
|x|=2
The absolute value equation |x|=2 gives us two possible values for x:
x=2orx=−2
Step 2: Solve for y
Next, we use the second equation:
|y|=x+1
We will consider both possible values of x from Step 1.
Case 1: If x=2:
|y|=2+1=3
This gives us two possible values for y:
y=3ory=−3
Case 2: If x=−2:
|y|=−2+1=−1
Since the absolute value cannot be negative, this case does not yield any valid solutions for y.
Step 3: Calculate y2
Now we will calculate y2 for the valid values of y from Case 1:
y=3⇒y2=32=9
y=−3⇒y2=(−3)2=9
Thus, the only possible value for y2 is:
y2=9
Final Answer
The possible value of y2 is 9.
---
We start with the equation:
12|x|=1
To eliminate the fraction, we multiply both sides by 2:
|x|=2
The absolute value equation |x|=2 gives us two possible values for x:
x=2orx=−2
Next, we use the second equation:
|y|=x+1
We will consider both possible values of x from Step 1.
|y|=2+1=3
This gives us two possible values for y:
y=3ory=−3
|y|=−2+1=−1
Since the absolute value cannot be negative, this case does not yield any valid solutions for y.
Now we will calculate y2 for the valid values of y from Case 1:
y=3⇒y2=32=9
y=−3⇒y2=(−3)2=9
y2=9
The possible value of y2 is 9.
Topper's Solved these Questions
Similar Questions
If x1,x2andy1,y2 are the roots of the equations
3x2−18x+9=0andy2−4y+2=0 the value of the determinant ∣∣ ∣ ∣∣x1x2y1y21x1+x2y1+y22sin(πx1x2)cos(π/2y1y2)1∣∣ ∣ ∣∣ is
View SolutionDefine the symbol # by the following equations:
x#y=(x−y)2, ifx>yx#y=x+y/4, ifx≤y
If x#y=−1, which of the following could be true?
View Solution
Knowledge Check
If 2x=2y+1, then which of the following could be true?
Ax>yBx<yCx=yD9x+12y=36If p(x)=|2−x|+12, which of the following could be the graph of y=p(x) ?
A B
B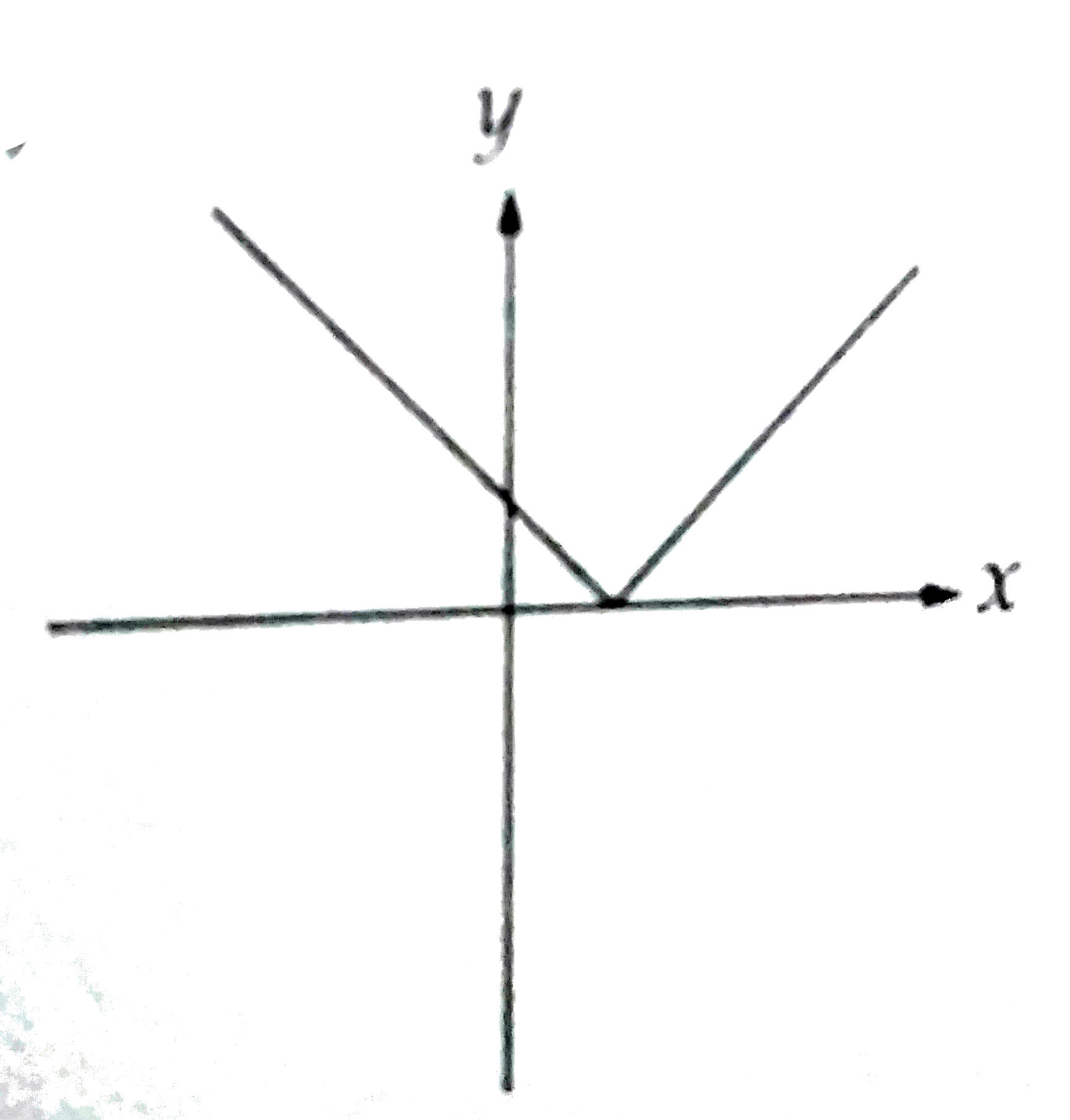 C
C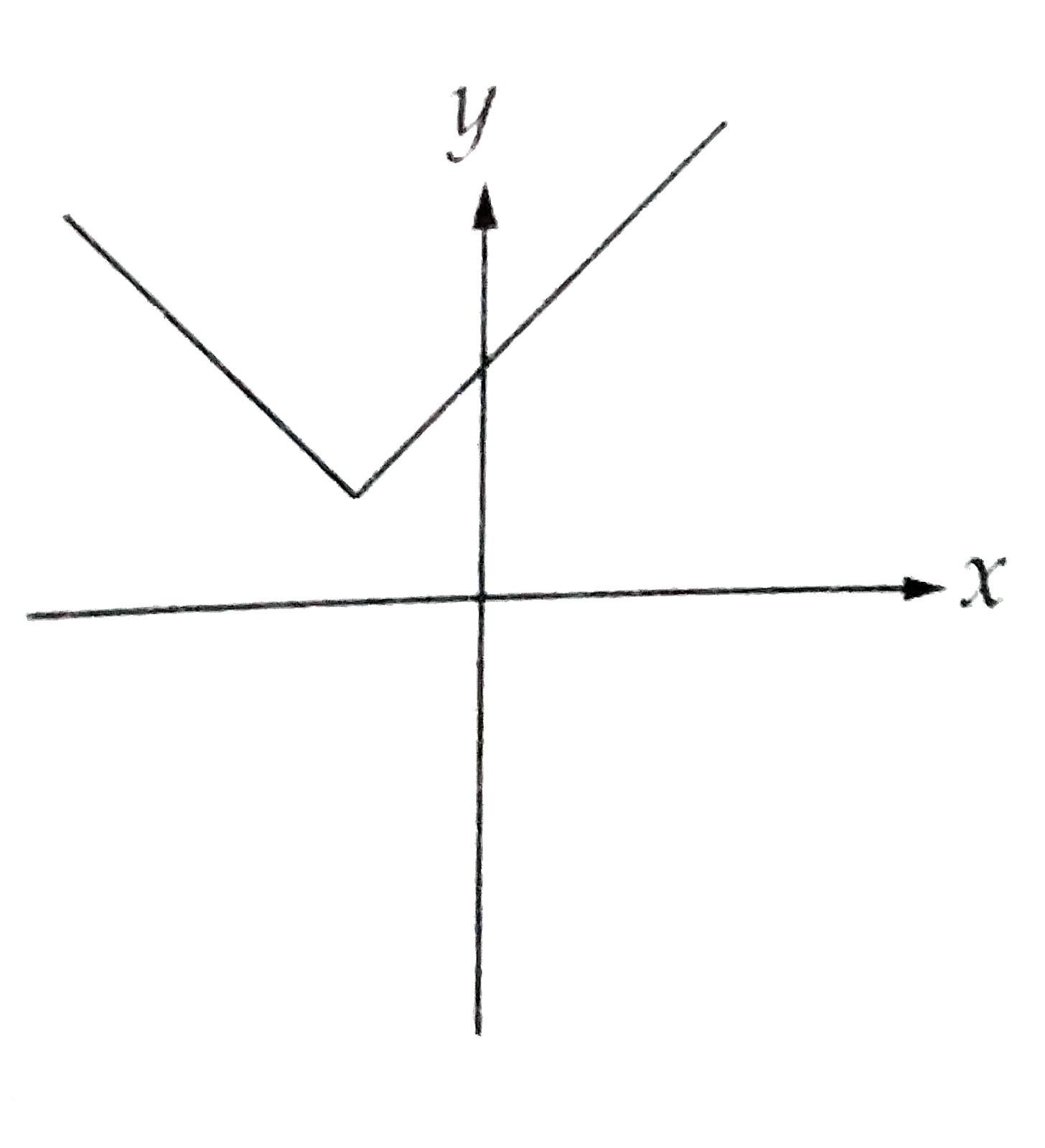 D
D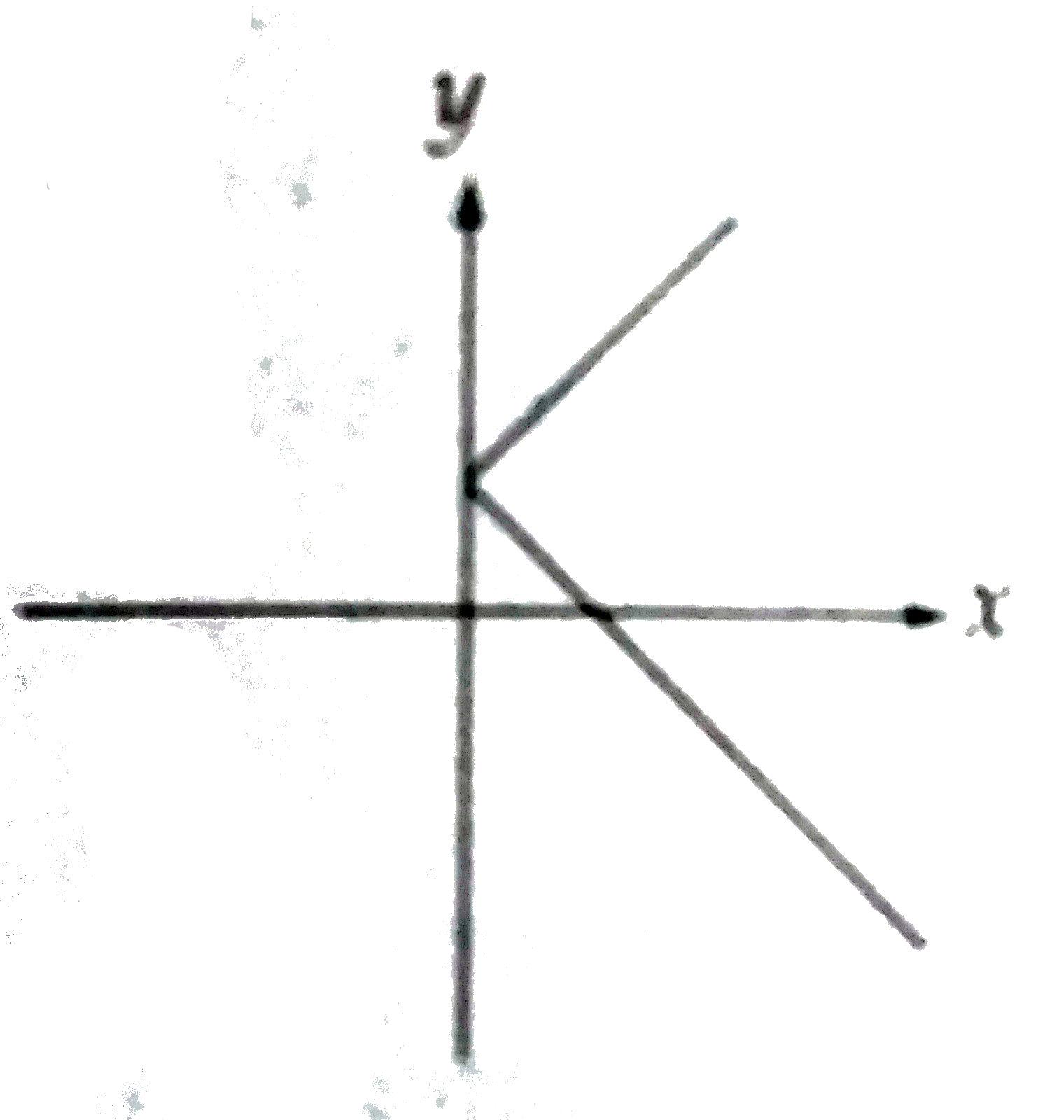
If the normals at (x1,y1) and (x2,y2) on y2=4ax meet again on parabola then x1x2+y1y2=
View SolutionIf (x1,y1) and (x2,y2) are the ends of a focal chord of the parabola y2 = 4ax then show that x1x2=a2,y1y2=−4a2
View SolutionIf y1n+y−1n=2x then (x2−1)y2+xy1 is equal to
View SolutionIf √1−x2+√1−y2=a(x−y), then prove that dydx=√1−y21−x2
View SolutionIf √1−x2+√1−y2=a(x−y), then prove that dydx=√1−y21−x2
View SolutionIf √1−x2+√1−y2=a(x−y), then prove that dydx=√1−y21−x2
View Solution
