The inequality |1.5C−24|≤30 represents the range of monthly average temperature, C, in degrees Celsius, during the winter month for a certain city. What was the lowest monthly average temperature, in degrees Celsius, for for this city?
−4
0
6
9
The correct Answer is:A
To solve the inequality |1.5C−24|≤30 and find the lowest monthly average temperature C in degrees Celsius for the city, we will follow these steps:
Step 1: Break down the absolute value inequality
The inequality |1.5C−24|≤30 can be rewritten as two separate inequalities:
−30≤1.5C−24≤30
Step 2: Solve the left part of the inequality
First, we solve the left part:
1.5C−24≥−30
Adding 24 to both sides:
1.5C≥−30+24
1.5C≥−6
Now, divide both sides by 1.5:
C≥−61.5
Calculating the right side:
C≥−4
Step 3: Solve the right part of the inequality
Now, we solve the right part:
1.5C−24≤30
Adding 24 to both sides:
1.5C≤30+24
1.5C≤54
Now, divide both sides by 1.5:
C≤541.5
Calculating the right side:
C≤36
Step 4: Combine the results
From the two parts, we have:
−4≤C≤36
Conclusion
The lowest monthly average temperature C for the city is:
−4
The inequality |1.5C−24|≤30 can be rewritten as two separate inequalities:
−30≤1.5C−24≤30
First, we solve the left part:
1.5C−24≥−30
Adding 24 to both sides:
1.5C≥−30+24
1.5C≥−6
Now, divide both sides by 1.5:
C≥−61.5
Calculating the right side:
C≥−4
Now, we solve the right part:
1.5C−24≤30
Adding 24 to both sides:
1.5C≤30+24
1.5C≤54
Now, divide both sides by 1.5:
C≤541.5
Calculating the right side:
C≤36
From the two parts, we have:
−4≤C≤36
The lowest monthly average temperature C for the city is:
−4
Topper's Solved these Questions
Similar Questions
A solution is to be kept between 300C and 350C . What is the range of temperature in degree Fahrenheit?
View SolutionIn drilling world's deepest hole it was found that the temperature T in degree Celsius, x Km below the earth's surface was given by T=30+25(x−3),3≤x≤15. At what depth will the temperature be between 155∘Cand205∘C?
View Solution
Knowledge Check
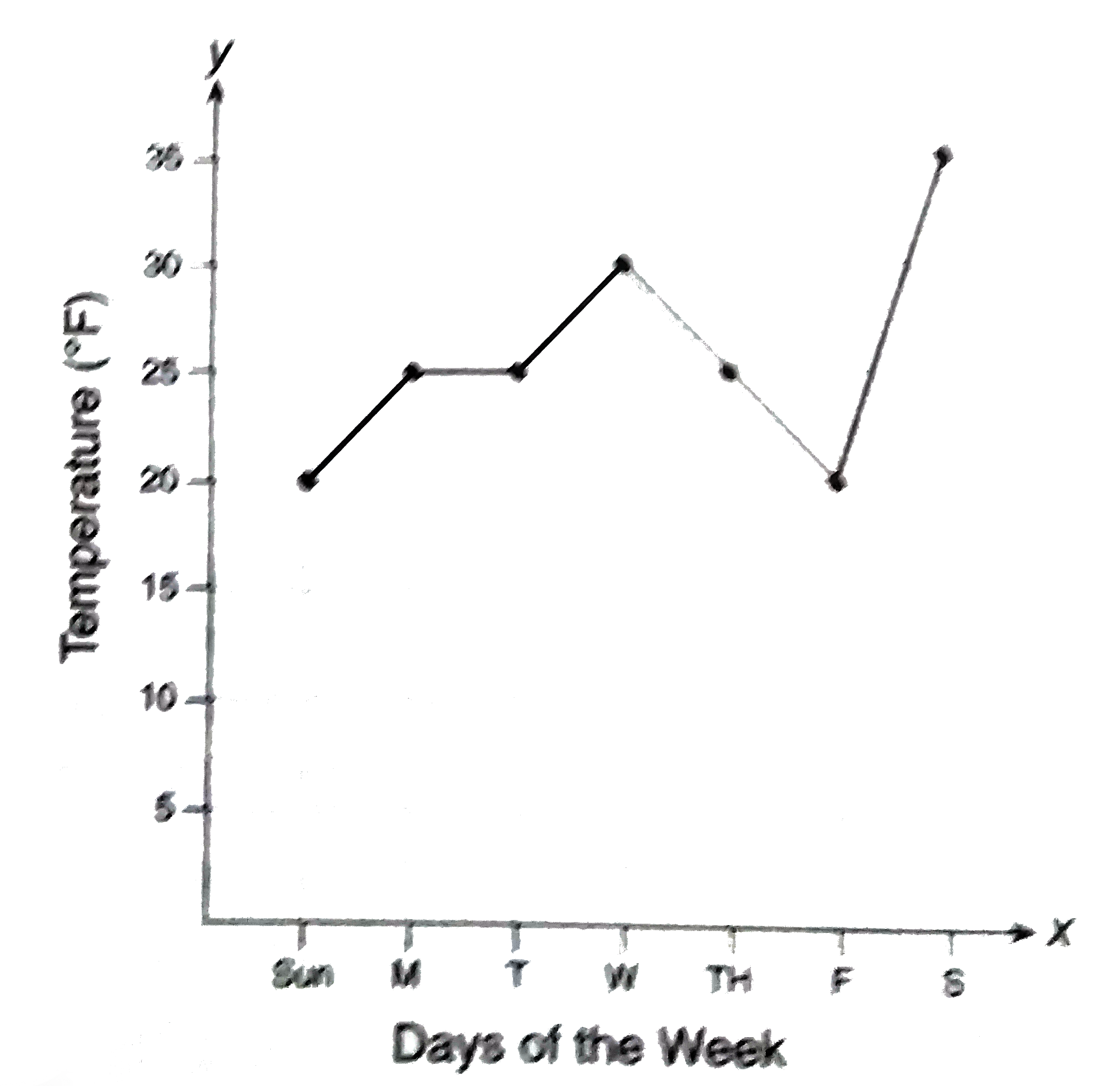
The graph above shows the average daily temperature during a particular week in January in certain city. Which statement best describes the temperature date in the graph above?AMedian=meanBmeas< modeCmedian =modeDmean=modeThe temperature, t, in degrees Fahrenheit, in a certain town on a certain spring day satisfies the inequality |t−24|≤30. Which of the followig temperatures , in degrees Fahrenheit, is NOT in this range?
A−10B−6C−5D0C=59(F−32)
The equation above shows how a temperature F, measured in degrees Fahrenheit, relates to a temperature C, measured in degrees Celsius. Based on the equation, which of the following must be true?
I. A temperature increase of 1 degree Fahrenheit is equivalent to a temperature increase of 59 degree Celsius.
II. A temperature increase of 1 degree Celsius is equivalent to a temperature increase of 1.8 degrees Fahrenheit.
III. A temperature increase of 59 degree Fahrenheit is equivalent to a temperature increase of 1 degree Celsius.AI onlyBII onlyCIII onlyDI and II only
A solution is be kept between 40∘Cand45∘C. What is the range of temperature in degree fahrenheit, if the conversion formula is F=95C+32?
View SolutionGiven that water freezes below zero degree celsius.
Consider the following statements :
p : water froze this morning , q : this morning temperature was below 0∘C
which of the following is correct ?
View SolutionA list kept at Town Hall contains the twon's average daily temperature in Fahrenheit, rounded to the nearest integer. A particular completed month has either 30 or 31 days. How many days does the month have?
(1) The median temperature is 73.5.
(2) The sum of the average daily temperature is divisible by 3.
View Solution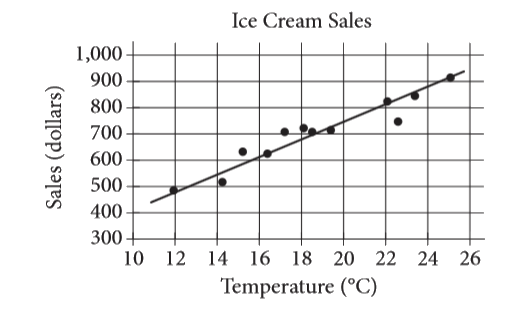
The scatterplot above shows a company’s ice cream sales d, in dollars, and the high temperature t, in degrees Celsius (.∘C), on 12 different days. A line of best fit for the data is also shown. Which of the following could be an equation of the line of best fit?
View SolutionThe relationship between temperature expressed in degrees fahrenheit (F) and degrees Celsius (C) is given by the formula
F=95C+32
If the temperature is 14 degrees Fahrenheit, what is it in degrees Celsius?
View Solution

