the pendulum on a clock swings through an angle 25∘, and the tip sweeps out an arc of 12 inches. How long is the pendulum?
1.67 inches
13.8 inches
27.5 inches
43.2 inches
The correct Answer is:C
To find the length of the pendulum, we can use the relationship between the arc length, the radius (length of the pendulum), and the angle in radians. Here’s a step-by-step solution:
Step 1: Understand the relationship
The formula that relates the arc length (s), the radius (r), and the angle in radians (θ) is given by:
s=r⋅θ
Where:
- s is the arc length (12 inches in this case),
- r is the length of the pendulum (which we need to find),
- θ is the angle in radians.
Step 2: Convert degrees to radians
We need to convert the angle from degrees to radians. The conversion formula is:
radians=degrees×π180
For our case:
θ=25∘×π180=25π180
Step 3: Simplify the angle in radians
We can simplify 25π180:
θ=25π180=5π36
Step 4: Substitute values into the formula
Now we can substitute the values into the arc length formula:
s=r⋅θ
Substituting s=12 inches and θ=5π36:
12=r⋅5π36
Step 5: Solve for the length of the pendulum (r)
To find r, we rearrange the equation:
r=12⋅365π
Step 6: Calculate the value
Now we can calculate the value:
r=4325π
Using π≈3.14:
r≈4325×3.14≈43215.7≈27.5 inches
Conclusion
The length of the pendulum is approximately 27.5 inches.
The formula that relates the arc length (s), the radius (r), and the angle in radians (θ) is given by:
s=r⋅θ
Where:
- s is the arc length (12 inches in this case),
- r is the length of the pendulum (which we need to find),
- θ is the angle in radians.
We need to convert the angle from degrees to radians. The conversion formula is:
radians=degrees×π180
For our case:
θ=25∘×π180=25π180
We can simplify 25π180:
θ=25π180=5π36
Now we can substitute the values into the arc length formula:
s=r⋅θ
Substituting s=12 inches and θ=5π36:
12=r⋅5π36
To find r, we rearrange the equation:
r=12⋅365π
Now we can calculate the value:
r=4325π
Using π≈3.14:
r≈4325×3.14≈43215.7≈27.5 inches
The length of the pendulum is approximately 27.5 inches.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The pendulum on a clock swings through an angle of 1 radian, and the tip sweeps out ann arc of 12 inches. How long is the pendulum?
A3.8 inchesB6 inchesC7.6 inchesD12 inchesThe bottom of a pendulum traces an arc 3 feet in length when the pendulum swings through an angle of 12 radians.What is the number of feet in the length of the pendulum?
A1.5B6C1.5πD6π
A car has two wipers which do not overlap. Each wiper has a blade of length 25 cm sweeping through an angle of 115∘ . Find the total area cleaned at each sweep of the blades.
View SolutionA wagon of mass M can move without friction along horizontal rails. A simple pendulum consisting of a sphere of mass m is suspended from the ceiling of the wagon by a string of length l. At the initial moment the wagon and the pendulum are at rest and the string is deflected through an angle α from the vertical. Find the velocity of the wagon when the pendulum passes through its mean position.
View SolutionA car has two wipers which do not overlap. Each wiper has a blade of length 25 cm sweeping through an angle of 115o . Find the total area cleaned at each sweep of the blades.
View SolutionFind the angle in radian through which a pendulum swings and its length is 75 cm and the tip describes an arc of length 21 cm.
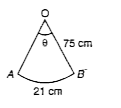
View SolutionFind the angle in radian through which a pendulum swings if its length is 75 cm and the tip describes an arc of length (i) 10 cm (ii) 15 cm (iii) 21 cm
View SolutionFind the angle in radian through which a pendulum swings if its length is 75 cm and the tip describes an arc of length (i) 10 cm (ii) 15 cm (iii) 21 cm
View Solution

