In △ABC,∠A=30∘,a=6andc=8. Which of the following must be true?
0∘<∠C<90∘
90∘<∠C<135∘
45∘<∠C<135∘
0∘<∠C<45∘ or 135∘<∠C<180∘
The correct Answer is:D
To solve the problem, we need to find the possible values of angle C in triangle ABC given that angle A = 30°, side a = 6, and side c = 8. We will use the sine rule to find the relationship between the sides and angles of the triangle.
1. Write down the Sine Rule:
The sine rule states that:
asinA=bsinB=csinC
Here, a is the side opposite angle A, b is the side opposite angle B, and c is the side opposite angle C.
2. Substitute the known values:
We know:
- A=30∘
- a=6
- c=8
Using the sine rule, we can set up the equation:
6sin30∘=8sinC
3. Calculate sin30∘:
We know that:
sin30∘=12
Therefore, substituting this into the equation gives:
612=8sinC
Simplifying the left side:
6×2=12
So we have:
12=8sinC
4. Cross-multiply to solve for sinC:
Cross-multiplying gives:
12sinC=8
Dividing both sides by 12:
sinC=812=23
5. Find angle C:
To find angle C, we take the inverse sine:
C=sin−1(23)
Using a calculator, we find:
C≈41.18∘
6. Consider the second possible angle:
Since sinC=23 can also correspond to an obtuse angle:
C=180∘−41.18∘≈138.82∘
7. Determine the range of angle C:
Thus, angle C can either be approximately 41.18∘ or 138.82∘. Therefore, the possible ranges for angle C are:
- From 0∘ to 90∘ (acute angle)
- From 90∘ to 180∘ (obtuse angle)
Conclusion:
The possible values for angle C are approximately 41.18∘ and 138.82∘. Thus, the correct option that must be true is that angle C can vary from 0∘ to 45∘ or from 135∘ to 180∘.
The sine rule states that:
asinA=bsinB=csinC
Here, a is the side opposite angle A, b is the side opposite angle B, and c is the side opposite angle C.
We know:
- A=30∘
- a=6
- c=8
6sin30∘=8sinC
We know that:
sin30∘=12
Therefore, substituting this into the equation gives:
612=8sinC
Simplifying the left side:
6×2=12
So we have:
12=8sinC
Cross-multiplying gives:
12sinC=8
Dividing both sides by 12:
sinC=812=23
To find angle C, we take the inverse sine:
C=sin−1(23)
Using a calculator, we find:
C≈41.18∘
Since sinC=23 can also correspond to an obtuse angle:
C=180∘−41.18∘≈138.82∘
Thus, angle C can either be approximately 41.18∘ or 138.82∘. Therefore, the possible ranges for angle C are:
- From 0∘ to 90∘ (acute angle)
- From 90∘ to 180∘ (obtuse angle)
The possible values for angle C are approximately 41.18∘ and 138.82∘. Thus, the correct option that must be true is that angle C can vary from 0∘ to 45∘ or from 135∘ to 180∘.
Topper's Solved these Questions
- TRIANGLE TRIGONOMETRY Book:ENGLISH SATChapter:TRIANGLE TRIGONOMETRY Exercise:EXERCISES
Explore 13 Videos
- TRANSFORMATION AND SYMMETRYBook:ENGLISH SATChapter:TRANSFORMATION AND SYMMETRYExercise:EXERCISES
Explore 4 Videos
- TRIGONOMETRIC FUNCTIONSBook:ENGLISH SATChapter:TRIGONOMETRIC FUNCTIONSExercise:MCQs (Exercise)
Explore 30 Videos
Similar Questions
Knowledge Check
If −3x+6≥18, which of the following must be true?
Ax≤−4Bx≤8Cx≥−4Dx≥−8If ln (xy)<0, which of the following must be true ?
Axy<0Bxy<1Cxy>1Dxy>0If f(x)=x3, which of the following must be true ?
Af(−x)=f(x)Bf(−x)=−f(−x)Cf(−x)=−f(x)Df(x)=−f(x)
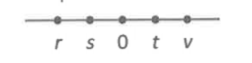
Which of the following MUST be true?
v>s+t
View SolutionIf x+y=90∘, which of the following must be true?
View SolutionIf ab>0, then which one of the following must be true?
View SolutionIf a+b>0 and c+d>0, which of the following must be true ?
View SolutionIf ab<0,a>b,andb>−b, which of the following must be true?
View Solution