Two lenses L1 and L2 are used to make a telescope. The larger lens L1 is a convex lens with both surfaces having radius of curvature equal to 0.5 m. The smaller lens L2 has two surfaces with radius of curvature 4 cm. Both the lenses are made of glass having refractive index 1.5. The two lenses are mounted in a tube with separation between them equal to 1 cm less than the sum of their focal length.
(a) Find the position of the image formed by such a telescope for an object at a distance of 100 m from the objective lens L1.
(b) What is the size of the image if object is 1 m high? Do you think that lateral magnification is a useful way to characterize a telescope?
(c) Angular magnification is defined as ratio of angle subtended by the image at the eyepiece to the angle subtended by the distant object at an unaided eye. Find the angular magnification of the above mentioned telescope.
The correct Answer is:(a) 8.8 cm from L2 in between the two lenses (b) 1.6 cm, No (c) 18.2
Step by step video, text & image solution for Two lenses L_(1) and L_(2) are used to make a telescope. The larger lens L_(1) is a convex lens with both surfaces having radius of curvature equal to 0.5 m. The smaller lens L_(2) has two surfaces with radius of curvature 4 cm. Both the lenses are made of glass having refractive index 1.5. The two lenses are mounted in a tube with separation between them equal to 1 cm less than the sum of their focal length. (a) Find the position of the image formed by such a telescope for an object at a distance of 100 m from the objective lens L_(1). (b) What is the size of the image if object is 1 m high? Do you think that lateral magnification is a useful way to characterize a telescope? (c) Angular magnification is defined as ratio of angle subtended by the image at the eyepiece to the angle subtended by the distant object at an unaided eye. Find the angular magnification of the above mentioned telescope. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:ARIHANTChapter:GEOMETRICAL OPTICSExercise:Level 3
Explore 9 Videos
- GEOMETRICAL OPTICSBook:ARIHANTChapter:GEOMETRICAL OPTICSExercise:Level 3
Explore 9 Videos
- ELECTROSTATICSBook:ARIHANTChapter:ELECTROSTATICSExercise:Level 3
Explore 59 Videos
- MAGNETIC EFFECT OF CURRENTBook:ARIHANTChapter:MAGNETIC EFFECT OF CURRENTExercise:Magnetic effect of Current
Explore 45 Videos
Similar Questions
The radius curvature of each surface of a convex lens of refractive index 1.5 is 40 cm. Calculate its power.
View SolutionThe refractive index of the material of a double convex lens is 1.5 and its focal length is 5cm .If the radii of curvature are equal the value of the radius of curvature ( in cms ) is
View Solution
Knowledge Check
The radius of curvature of each surface of a lens is 40 cm. Its refractive index is 1.5. The focal length of lens will be
A40 cmB20 cmC80 cmD30 cmThe radius of curvature for a convex lens is 40 cm , for each surface. Its refractive index is 1.5. The focal length will be
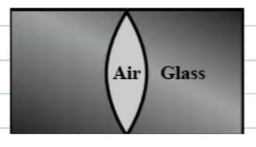
A40 cmB20 cmC80 cmD30 cmIn figure, an air lens of radius of curvature of each surface equal to 10cm is cut into a cylinder of glass of refractive index 1.5. The focal length and the nature of lens are
A15cm divergingB15cm convergingC10cm divergingD10cm converging
A planoconvex lens is made of refractive index 1.6. The radius of curvature of curved surface is 60 cm. The focal length of the lens is
View SolutionA plano convex lens is made of glass of refractive index 1.5. The radius of curvature of its convex surface is R. Its focal length is
View SolutionA plano-convex lens has refractive index 1.6 and radius of curvature 60 cm. What is the focal length of the lens?
View SolutionA plano-convex lens is made of glass of refractive index 1.5. The radius of curvature of its convex surface is R. Its focal length is
View SolutionA plano-convex lens is made of glass of refractive index 1.5. the radius of curvature of its convex surface is R. its focal length is
View Solution