The refractive index of light in glass varies with its wavelength according to equation
μ(λ)=a+bλ2 where a and b are positive constants.
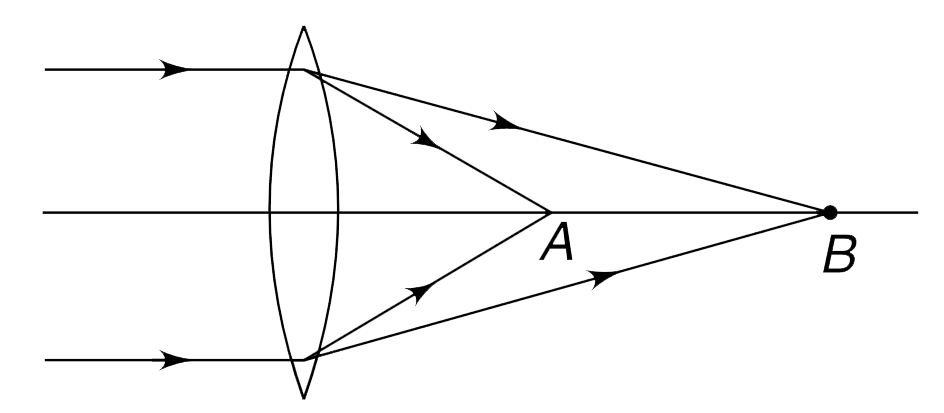
A nearly monochromatic parallel beam of light is incident on a thin convex lens as shown. The wavelength of incident light is λ0±Δλ where Δλ<<λ0. The light gets focused on the principal axis of the lens over a region AB. If the focal length of the lens for a light of wavelength λ0 is f0, find the spread AB.
The correct Answer is:f0[4bΔλλ0(aλ20+b−λ20)]
Step by step video, text & image solution for The refractive index of light in glass varies with its wavelength according to equation mu (lambda) = a+ (b)/(lambda^(2)) where a and b are positive constants. A nearly monochromatic parallel beam of light is incident on a thin convex lens as shown. The wavelength of incident light is lambda_(0) +-Delta lambda where Delta lambda lt lt lambda_(0). The light gets focused on the principal axis of the lens over a region AB. If the focal length of the lens for a light of wavelength lambda_(0) is f_(0), find the spread AB. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:ARIHANTChapter:GEOMETRICAL OPTICSExercise:Level 3
Explore 9 Videos
- GEOMETRICAL OPTICSBook:ARIHANTChapter:GEOMETRICAL OPTICSExercise:Level 3
Explore 9 Videos
- ELECTROSTATICSBook:ARIHANTChapter:ELECTROSTATICSExercise:Level 3
Explore 59 Videos
- MAGNETIC EFFECT OF CURRENTBook:ARIHANTChapter:MAGNETIC EFFECT OF CURRENTExercise:Magnetic effect of Current
Explore 45 Videos
Similar Questions
The refractive index μ of a medium is found to vary with wavelength λ as μ=A+Bλ2. What are the dimensions of A and B?
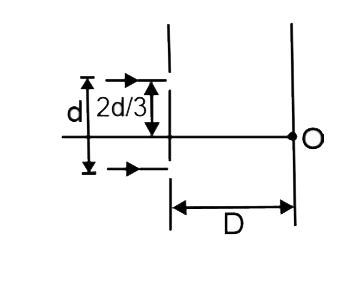
View SolutionIn the figure shown if a parallel beam of white light is incident on the plane of the slits then the distance of the white spot on the screen from O is [Assume <<D,λ<<d]
View Solution
Knowledge Check
The refractive index of a medium is given by μ=A+Bλ2 where A and B are constants and λ is the wavelength of light.
Then the dimensions of B are the same as that ofAWavelengthBAreaCVolumeDVelocityCalculate the work function of the metal, if the kinetic energies of the photoelectrons are E1 and E2, with wavelengths of incident light λ1 and λ2
AE1λ1−E2λ2λ2−λ1BE1E2λ1−λ2C(E1−E2)λ1λ2(λ1−λ2)Dλ1λ2E1(λ1−λ2)E2The wavelength of light in air and some other medium are respectively λa and λm. The refractive index of medium is
Aλa/λmBλm/λaCλa×λmDNone of these
A monochromatic light of wavelength λ is incident on an isolated metalic sphere of radius a. The threshold wavelength is λ0 which is larger then λ. Find the number of photoelectrons emitted before the emission of photo electrons stops.
View SolutionA light filter is a plate of thickness d whose absorption coefficient depends on wavelength λ as
x(λ)=α(1−λ/λ0)2cm−1,
where α and λ0 are constants. Find the passband Δλ of this light filter, that is the band at whose edge the attenuation of light is η times that at the wavelength λ0. The coefficient of reflection from teh surfaces of the light filter is assumed to be the same at all wavelengths.
View SolutionIn Young's double-slit experiment, two wavelengths of light are used simultaneously where λ2=2λ1. In the fringe pattern observed on the screen,
View SolutionWhen light of wavelength λ travels through glass, the refractive index of glass varies with wavelength as μ=A+Bλ2. What are the dimensional formulae of A and B?
View SolutionA beam of light is incident at polarising angle θ on air-glass interface. If λaandλg are the wavelength of light in air and glass respectively then
View Solution

