The Figure shows the equatorial circle of a glass sphere of radius R having centre at C. The eye of an observer is located in the plane of the circle at a distance R from the surface. A small insect is crawling along the equatorial circle.
(a) Calculate the length (L) of the are on the circle where the insect lies where its image is visible to the observer.
(b) Calculate the value of L when the eye is brought very close to the sphere. Refractive index of the glass is μ=1√2
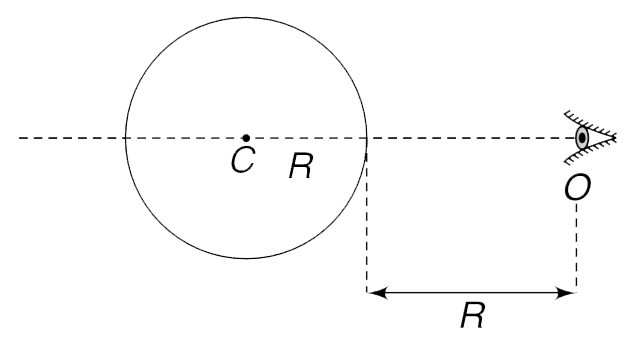
The Figure shows the equatorial circle of a glass sphere of radius R having centre at C. The eye of an observer is located in the plane of the circle at a distance R from the surface. A small insect is crawling along the equatorial circle. (a) Calculate the length (L) of the are on the circle where the insect lies where its image is visible to the observer. (b) Calculate the value of L when the eye is brought very close to the sphere. Refractive index of the glass is mu =(1)/(sqrt(2))

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:(a) πR3 (b) πR

Updated on:21/07/2023
|
Answer

Step by step video, text & image solution for The Figure shows the equatorial circle of a glass sphere of radius R having centre at C. The eye of an observer is located in the plane of the circle at a distance R from the surface. A small insect is crawling along the equatorial circle. (a) Calculate the length (L) of the are on the circle where the insect lies where its image is visible to the observer. (b) Calculate the value of L when the eye is brought very close to the sphere. Refractive index of the glass is mu =(1)/(sqrt(2)) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023
Class 12PHYSICSRAY OPTICS AND OPTICAL INSTRUMENTS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Calculate the length (in cm) of the chord of the circle which is at the distance of the 12 cm from the centre and at the radius of the circle is 13 cm.

    A10
    B12
    C13
    D15

  • From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of circle is :

    A7 cm
    B12 cm
    C15 cm
    D24.5 cm

  • If the distance of point P from the centre of the circle is 13 cm and the radius of the circle is 5 cm, then length of the tangent drawn from P to the circle is :

    A8 cm
    B6.5 cm
    C9 cm
    D12 cm.