ISOSCELES TRIANGLE A triangle whose two sides are equal is called an isosceles triangle.
Isosceles Triangle
In this chapter, we will focus on the isosceles triangle. Students would be able to learn about the area of an isosceles triangle as well as isosceles triangle formula. We would also concentrate on the isosceles triangle properties. Students would be able to work on the solved examples that would help to get the best idea about it.
What is an Isosceles Triangle?
A triangle that has any of its two sides equal to each other is called an isosceles triangle. The opposite sides of the angles are equal. It is based on the angles and sides when the classifications of the types of triangles are done. A triangle is classified into three types based on the sides, namely isosceles, scalene and equilateral. Based on the angles, the classification of the triangle is done in three types which are obtuse-angled, acute-angled and right-angled.
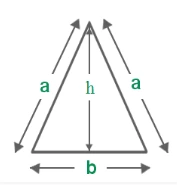
Isosceles Triangle Properties
- The two sides of an isosceles triangle are equal, whereas the base of the triangle is the unequal side.
- The angles which are opposite to the two equal sides of the triangle are always equal.
- The measurement from the base to the vertex (topmost) of the triangle is the altitude of an isosceles triangle.
- The right-angled isosceles triangle has the third angle as 90 degrees.
Isosceles Triangle Area Formula
The formula of an isosceles triangle is ½ x b x h where b and h are the base and height of the triangle respectively.
So A = ½ x b x h
Isosceles Triangle Perimeter Formula
We are familiar that the boundary of the shape is the perimeter of any shape. It is through the knowledge of its base and side that the perimeter of an isosceles triangle can be found.
So, P = 2a + b where the two equal sides of the triangle is ‘a’ and the base of the triangle is ‘b’.
Related Videos:
It is important to solve different problems related to the isosceles triangle. We will have a look at some of the solved questions to get some good idea.
Problem 1: Determine the area of an isosceles triangle whose height is 9 cm and base as 6 cm?
Solution: Area of an isosceles triangle is ½ × b × h
A = ½ × 9 × 6 = 27 cm2
Problem 2: Find the perimeter of an isosceles triangle, with side 8 cm and base 6cm.
Solution: P = 2a + b = 2(8) + 6 = 16 + 6 = 22 cm
Problem 3: An isosceles triangle has an area 20 unit with 2 and base 10 units. Can you find its lateral side?
Solution: Given b =10
Now, we use the formula of area of isosceles triangle
A = (1/2) b h = 20
h = 40 / 10 = 4
Now, by making use of Pythagoras theorem, we get
a 2 = (b/2) 2 + h 2 = √ ( 5 2 + 4 2) = √41
Problem 4: The height h (perpendicular to its base b) of the isosceles triangle is 4 cm shorter than its base b, and its area is 30 cm2? What is the lateral side of it?
Solution: We use the formula of area of the isosceles triangle
A = (1/2) b h = 30
h = b - 4 (given)
Now, we need to substitute h by b - 4 in the formula for A
Here, we get
A = (1/2) b (b - 4) = 30
We get the equation: b 2 - 4 b - 60 = 0
Now, solutions to the equation: b = 10 and b = - 6
so, b is a length and therefore is positive where h = b - 4 = 6 ( b = 10),
a = √ (h 2 + (b/2) 2)=
So √ (36 + 25) = √61
Problem 5: ABC and BCD are isosceles triangles. Determine the angle BDE?
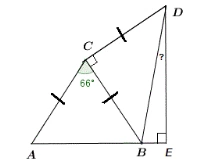
Solution: We can see that ABC is an isosceles triangle,
So, ∠CAB = ∠ABC
it is also found that
∠CAB + ∠ABC = 180 - 66
now, 2 ∠ABC = 180 - 66
we get: ∠ABC = 57°
BCD is a right isosceles triangle; so,
∠CBD = ∠CDB = (180 - 90)/2 = 45°
We find that ∠ABC, ∠CBD and ∠DBE make a straight angle. Therefore,
∠ABC + ∠CBD + ∠DBE = 180°
we get ∠DBE = 180 - ∠ABC - ∠CBD = 180 - 57 - 45 = 78°
Here, DBE is a right triangle,
Therefore ∠BDE = 90 - 78 = 12°
Important Chapters:


Similar Questions
ISOSCELES TRIANGLE A triangle whose two sides are equal is called an isosceles triangle.
View SolutionArea of an isosceles triangle
View SolutionScalene Triangle a triangle whose no two sides are equal is called a scalene triangle.
View SolutionA triangle whose two sides are equal is known as acute triangle (b) an isosceles triangle a scalene triangle (d) a right triangle
View SolutionA triangle whose on two sides are equal is called an acute triangle (b) a scalene triangle an isosceles triangle (d) an equilateral triangle
View SolutionSymmetry of an isosceles triangle
View SolutionA triangle whose all sides are equal is called an equilateral triangle (b) an acute triangle a right triangle (d) an isosceles triangle
View SolutionThe angles opposite to equal sides of an isosceles triangle are ..........
View SolutionLines of symmetry of an isosceles triangle
View SolutionLines of symmetry of an isosceles triangle
View Solution

