Area of an isosceles triangle
Area of an Isosceles Triangle
We will figure out how to determine the area of an isosceles triangle. We'll additionally see how to find the height of an isosceles triangle given the lengths of its sides since this is required to determine the area of a triangle.
Fundamentals of Isosceles Triangle
It is helpful to characterize an isosceles triangle to determine the area of an isosceles triangle. An isosceles triangle has only two sides of equivalent length, similar to the one depicted below.
As a rule, with regards to a triangle, we have a decent equation that we can use to determine the area of the triangle. The particular formula is applicable for all triangles. Be that as it may, before we look into the formula, we should initially acquaint ourselves with the various parts of an isosceles triangle.
In an isosceles triangle, we consider the two equivalent sides as the legs of the triangle, and we consider the opposite side as the triangle base. The points on which the sides of the triangle meet are called vertices. The length from the centre point of the base to the vertex is known as the height of the triangle.
Formula of Area of an Isosceles Triangle
Until now, we have made ourselves familiar with different parts of an isosceles triangle, let's concentrate on the whole part. To calculate the area of an isosceles triangle, we use the below formula:
where A is the area:
A = (1/2) base x height
For instance, consider an isosceles triangle with a base of 10 centimetres and a height of 12 centimetres, we would put the values, b = 10 and h = 12 into the formula to determine the area, like this:
A = (1/2) b x h
A = (1/2) x 10cm x 12cm
A = 60 cm2
We determined that the area of an isosceles triangle with base 10 centimetres and height 12 centimetres is 60 square centimetres.
Determination of Height of Isosceles Triangle
We have figured out that finding the area of an isosceles triangle is equivalent to finding the area of any triangle - we utilize the equation for the area of a triangle, A = (1/2) b x h. In any case, we frequently aren't given the height of an isosceles triangle, and we unquestionably need this to apply the formula. It is significantly more typical that we would have the lengths of the base and other sides of an isosceles triangle than it is that we would have the height of the triangle.
For instance, assume you purchase a state park sticker for the windshield of your vehicle that is looking like an isosceles triangle. The sticker provides the lengths of its sides as 9cm, 9cm and 7cm. It does not indicate the height or the area of the sticker, and you need to find the area to realize how a lot of room it will take up on your windshield. The length of the base is 7 centimetres, so to determine the area you should find the height of the sticker.
The line depicting the height of an isosceles triangle crosses the base so that it cut the base down from the middle. This divides the triangle into two right triangles.
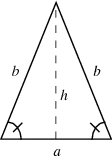
In light of that, we can utilize the Pythagorean hypothesis, which expresses that if a and b are the legs of a right-angled triangle and c is the hypotenuse (or the longest side), at that point a2 + b2 = c2. We can utilize this to find the height.

As a rule, with regards to a triangle, we have a decent equation that we can use to determine the area of the triangle. The particular formula is applicable for all triangles. Be that as it may, before we look into the formula, we should initially acquaint ourselves with the various parts of an isosceles triangle.

Similar Questions
Knowledge Check
The ratio of the area of two isosceles triangles having the same vertical angle (i.e. angle between equal sides) is 1:4. The ratio of their heights is
A1:4B2:5C1:2D3:4Vertices of an isosceles triangle of area a2 are (-a,0) and (a,0). Equation of the circumcircle of the triangle is
Ax2+y2+2ax−2ay+a2=0Bx2+y2−2ax+2ay+a2=0Cx2+y2=a2Dnone of theseThe perimeter of an isosceles triangle is equal to 14 cm and the lateral side is to the base in the ratio 5 : 4. The area of the triangle is (a) 21 cm2 (b) 0.5√21cm2 (c) 1.5√21cm2 (d) 2√21cm2
A12√21cm2B32√21cm2C√21cm2D2√21cm2
The base of an isosceles triangle is 300 units and each of its equal sides is 170 units. Then the area of the triangle is
View SolutionThe base of an isosceles triangle is 48 cm and one of its equal sides is 30 cm. Find the area of the triangle
View SolutionThe base of an isosceles triangle measures 24 cm and its area is 192cm2 , Find its perimeter.
View SolutionThe base of an isosceles triangle is 16 cm. If both the equal sides be 17 cm each, find the area of the triangle.
View SolutionThe base of an isosceles triangle is 12cm and its area is 48 cm2. Find the equal sides of the triangle.
View Solution

