A balloon rises up with constant net acceleration of 10m/s2. After 2 s a particle drops from the balloon. After further 2 s match the following : (Takeg=10m/s2)
Column IColumn II(A)Height of perticle from ground(p)Zero(B)Speed of particle(q)10SIunits(C)Displacement of Particle(r)40SIunits(D)Acceleration of particle(s)20SIunits
The correct Answer is:(A)-r, (B)-p, (C)-s, (D)-q
To solve the problem step by step, we need to analyze the motion of the balloon and the particle that drops from it.
Step 1: Analyze the motion of the balloon
The balloon rises with a constant net acceleration of 10m/s2. We need to find the velocity of the balloon after 2 seconds.
Using the first equation of motion:
V=U+at
Where:
- U=0m/s (initial velocity of the balloon)
- a=10m/s2 (acceleration of the balloon)
- t=2s
Substituting the values:
V=0+(10×2)=20m/s
Step 2: Calculate the height of the balloon after 2 seconds
Using the second equation of motion to find the displacement S1 of the balloon:
S=Ut+12at2
Substituting the values:
S1=0×2+12×10×(22)=0+12×10×4=20m
Step 3: Analyze the motion of the particle after it drops
When the particle drops from the balloon after 2 seconds, it has an initial velocity equal to the velocity of the balloon at that moment, which is 20m/s upward.
Step 4: Determine the motion of the particle in the next 2 seconds
The particle will experience downward acceleration due to gravity (g=10m/s2). We need to find the final velocity V of the particle after 2 seconds of free fall.
Using the first equation of motion:
V=U+at
Where:
- U=20m/s (initial velocity of the particle)
- a=−10m/s2 (acceleration due to gravity, negative because it is downward)
- t=2s
Substituting the values:
V=20+(−10×2)=20−20=0m/s
Step 5: Calculate the displacement of the particle during the 2 seconds
Using the second equation of motion to find the displacement S2 of the particle:
S=Ut+12at2
Substituting the values:
S2=20×2+12×(−10)×(22)=40−20=20m
Step 6: Total height of the particle from the ground
The total height of the particle from the ground is the height of the balloon plus the displacement of the particle:
Height=S1+S2=20+20=40m
Step 7: Final results
1. Height of particle from ground: 40m
2. Speed of particle after 4 seconds: 0m/s
3. Displacement of particle: 0m (since it returns to the same height it was dropped)
4. Acceleration of particle: 10m/s2 downward (due to gravity)
Summary of Results
- Height of particle from ground: 40m (matches with option (r))
- Speed of particle: 0m/s (matches with option (p))
- Displacement of particle: 0m (matches with option (q))
- Acceleration of particle: 10m/s2 (matches with option (s))
The balloon rises with a constant net acceleration of 10m/s2. We need to find the velocity of the balloon after 2 seconds.
V=U+at
Where:
- U=0m/s (initial velocity of the balloon)
- a=10m/s2 (acceleration of the balloon)
- t=2s
V=0+(10×2)=20m/s
Using the second equation of motion to find the displacement S1 of the balloon:
S=Ut+12at2
Substituting the values:
S1=0×2+12×10×(22)=0+12×10×4=20m
When the particle drops from the balloon after 2 seconds, it has an initial velocity equal to the velocity of the balloon at that moment, which is 20m/s upward.
The particle will experience downward acceleration due to gravity (g=10m/s2). We need to find the final velocity V of the particle after 2 seconds of free fall.
V=U+at
Where:
- U=20m/s (initial velocity of the particle)
- a=−10m/s2 (acceleration due to gravity, negative because it is downward)
- t=2s
V=20+(−10×2)=20−20=0m/s
Using the second equation of motion to find the displacement S2 of the particle:
S=Ut+12at2
Substituting the values:
S2=20×2+12×(−10)×(22)=40−20=20m
The total height of the particle from the ground is the height of the balloon plus the displacement of the particle:
Height=S1+S2=20+20=40m
1. Height of particle from ground: 40m
2. Speed of particle after 4 seconds: 0m/s
3. Displacement of particle: 0m (since it returns to the same height it was dropped)
4. Acceleration of particle: 10m/s2 downward (due to gravity)
- Height of particle from ground: 40m (matches with option (r))
- Speed of particle: 0m/s (matches with option (p))
- Displacement of particle: 0m (matches with option (q))
- Acceleration of particle: 10m/s2 (matches with option (s))
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - KINEMATICSEXERCISE - Assertion-Reason20videos
KINEMATICS
- BOOK - ALLENCHAPTER - KINEMATICSEXERCISE - Comprehension#13videos
KINEMATICS
- BOOK - ALLENCHAPTER - KINEMATICSEXERCISE - EXERCISE-0257videos
KINEMATICS
- BOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)22videos
ERROR AND MEASUREMENT
- BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-78videos
KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
Similar Questions
For the velocity -time graph shown in figure, in a time interval from t=0 to t=6s, match the following:
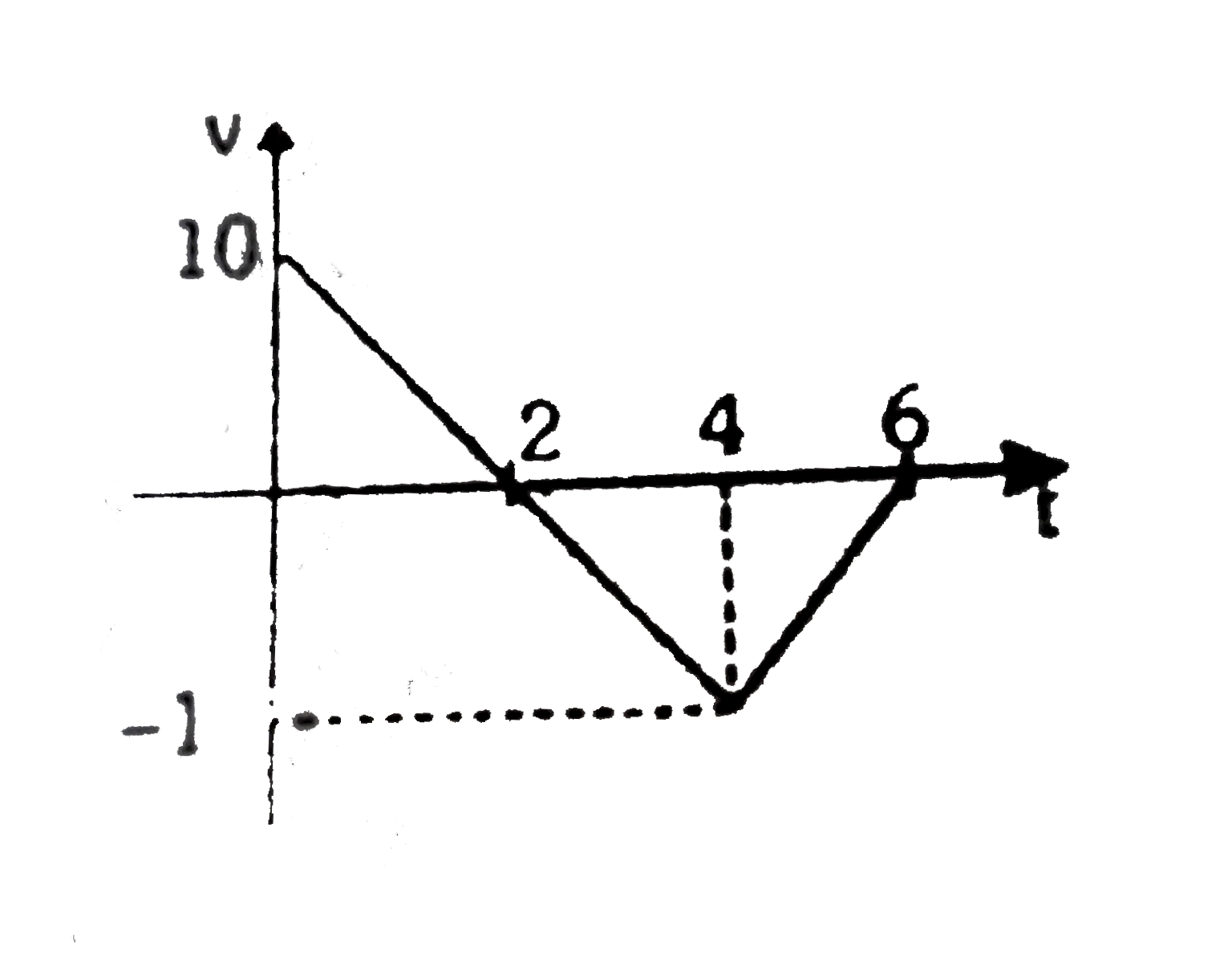
Column IColumn II(A)Change in velocity(p)−5/3SIunit(B)Average acceleration(q)−20SIunit(C)Total displacement(r)−10SIunit(D)Acceleration ay t=3s(s)−5SIunitView SolutionA balloon starts rising from the ground with a constant acceleration of 1.25m/s2. After 8 s, a stone is released from the balloon. Find the time taken by the stone to reach the ground. (Take g=10m/s2)
View Solution
Knowledge Check
- Question 1 - Select One
A balloon os mass 2 KG is rising up with an acceleration of 4ms2 . The upward force acting on the balloon is (g=10ms−2
A0.8 kgfB2.8 kgfC2.4 kgfD2.0 kgf - Question 2 - Select One
A ballon is ascending with a constant velocity of 20 m/s. A particle is dropped from it when its height was 60m above the ground. Find if (g=10m/s2). The time of flight of particle
A4 sB5sC3sD6s
In the diagram shown in figure, match the following columns (take g=10ms−2)

Column IColumn II(A) Normal reaction(p) 12 SI unit(B) Force of friction(q) 20 SI unit(C) Acceleration of block(r) zero(s) 2 SI unitView SolutionIn the diagram shown in figure, match the following (g=10m/s2)

Column-IColoumn-II(A)Acceleration of 2kg block(P)8 Si unit(B)Net force on 3kg block(Q)25 SI unit(C)Normal reaction between 2 kg and 1kg(R)2 SI unit(D)Normal reaction between 3 kg and 2kg (S) 45 SI unit(T) NoneView SolutionIn the s-t equation (s=10+20t−5t2) match the following columns.
∣∣ ∣ ∣ ∣ ∣ ∣∣Column IColumn II(A)Distancec travelled in 3s(p)−20 units(B)Displacement 1 s(q)15 units(C)Initial acceleration(r)25 units(D)Velocity at 4 s(s)−10 units∣∣ ∣ ∣ ∣ ∣ ∣∣View SolutionA balloon of mass 2 kg is rising up with an acceleration of 4ms2. The upward force acting on the balloon is (g=10ms−2)
View SolutionA particle of mass 1 kg is projected upwards with velocity 60ms−1. Another particle of mass 2kg is just dropped from a certain height. After 2s, match the following.
[Take, g =10ms−2]
column1column2Accelertion of CMP ZeroB Velocity of CMQ 10 SI unitC Displacement of CM20 SI unit-S NoneView SolutionA particle is rotating in a circle of radius 1m with constant speed 4m/s. In time 1s, match the following (in SI units)
Column IColumn II(A)Displacement(p)8sin2(B)Distance(q)4(C)Average velocity(r)2sin2(D)Average acceleration(s)4sin2View Solution

